练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    方程2x-x2=
    2x
    的正根个数为
     
    个．
    分析：根据方程的根与对应函数零点的辩证关系，我们可以将方程2x-x2=
    2
    x
    的正根个数转化为函数正零点的个数问题，在同一坐标系中分别画出函数y=2x-x2，y=
    2
    x
    的图象，利用交点法，即可得到结论．
    解答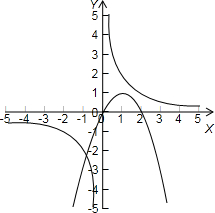：精英家教网解：在同一坐标系中分别画出函数y=2x-x2，y=
    2
    x
    的图象，如下图所示：
    由图可知，两个函数的图象只有一个交点，且横坐标为负
    即方程2x-x2=
    2
    x
    无正根，
    故答案为：0
    点评：本题考查的知识点是根的存在性及根的个数判断，其中根据函数的根与对应函数零点的辩证关系，将方程正根个数转化为函数正零点的个数问题，是解答本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知方程（x2-2x+m）（x2-2x+n）=0的四个根组成一个首项为
    1
    4
    的等差数列，则|m-n|等于（　　）
    A、1
    B、
    3
    4
    C、
    1
    2
    D、
    3
    8

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    方程y=-
    		x2-2x+1
    表示的曲线是（　　）
    A、双曲线B、半圆
    C、两条射线D、抛物线

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    方程2x-x2=
    2
    x
    的正根个数为（　　）
    A、0B、1C、2D、3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    三次方程x3+x2-2x-1=0的根不可能在的区间为（　　）

    查看答案和解析>>

    同步练习册答案