在等差数列{an}中,a8=0,a4=4,数列{bn}满足b1=1,bn-bn-1=an,则b10=________.
分析:设公差为d,由等差数列的通项公式求出首项和公差d的值,可得{a
n}的通项公式,根据递推关系 b
1=1,b
n-b
n-1=a
n =8-n,累加求出b
10的值.
解答:等差数列{a
n}中,a
8=0,a
4=4,设公差为d,则有 0-4=4d,解得d=-1.再由a
4=4=a
1+3d,可得 a
1=7,∴a
n =7+(n-1)(-1)=8-n.
再由 b
1=1,b
n-b
n-1=a
n =8-n,可得 b
1=1,b
2-b
1=8-2,b
3-b
2=8-3,b
4-b
3=8-4,…b
10-b
9=8-10,
累加可得 b
10=1+(8-2)+(8-3)+(8-4)+…+(8-10)=1+9×8-(2+3+4+…+10)=73-
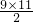
=
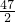
,
故答案为
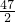
.
点评:本题主要考查等差数列的定义和性质,等差数列的通项公式,等差数列的前n项和公式的应用,属于中档题.

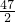
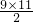 =
=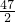 ,
,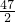 .
.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案