
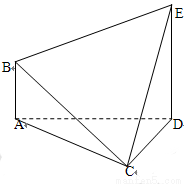
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1。
(1)请在线段CE上找到一点F,使得直线BF∥平面ACD,并证明;
(2)求平面BCE与平面ACD所成锐二面角的大小;
(1)详见解析;(2)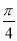
【解析】
试题分析:(1)若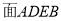 的线
的线 ∥面
∥面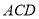 ,且
,且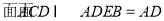 ,由线面平行的性质定理可知
,由线面平行的性质定理可知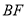 ∥
∥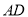 , 即若证得
, 即若证得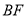 ∥
∥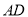 ,则可证得
,则可证得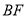 ∥面
∥面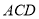 。由已知可知
。由已知可知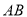 ∥
∥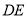 且
且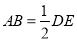 ,则点
,则点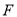 为
为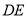 中点时根据平行四边形可证得
中点时根据平行四边形可证得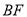 ∥
∥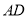 。(2)设所求的二面角的大小为
。(2)设所求的二面角的大小为 ,则
,则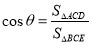 。(也可用空间向量法)
。(也可用空间向量法)
解法一:以D点为原点建立如图所示的空间直角坐标系,使得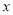 轴和
轴和 轴的正半轴分别经过点A和点E,则各点的坐标为
轴的正半轴分别经过点A和点E,则各点的坐标为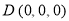 ,
,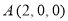 ,
,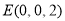 ,
,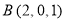 ,
,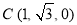 ,
,
(1)点F应是线段CE的中点,下面证明:
设F是线段CE的中点,则点F的坐标为
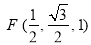 ,∴
,∴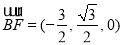
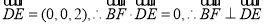 ,而
,而 是平面ACD的一个法向量,
是平面ACD的一个法向量,
此即证得BF∥平面ACD; 6分
(2)设平面BCE的法向量为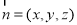 ,则
,则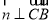 ,且
,且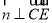 ,
,
由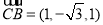 ,
,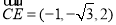 ,
,
∴ ,不妨设
,不妨设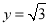 ,则
,则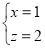 ,即
,即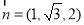 ,
,
∴所求角 满足
满足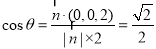 ,∴
,∴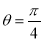 ; 13分
; 13分
解法二:(1)由已知AB⊥平面ACD,DE⊥平面ACD,∴AB//ED,
设F为线段CE的中点,H是线段CD的中点,
连接FH,则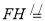
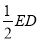 ,∴
,∴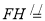
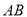 ,
,
∴四边形ABFH是平行四边形,∴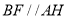 ,
,
由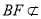 平面ACD内,
平面ACD内,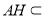 平面ACD,
平面ACD,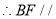 平面ACD
平面ACD
(2)由已知条件可知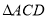 即为
即为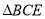 在平面ACD上的射影,设所求的二面角的大小为
在平面ACD上的射影,设所求的二面角的大小为 ,则
,则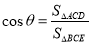 ,
,
易求得BC=BE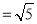 ,CE
,CE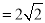 ,∴
,∴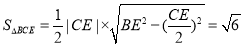 ,
,
而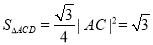 ,∴
,∴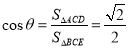 ,且
,且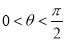 , ∴
, ∴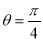
考点:1线线平行、线面平行;2二面角。


科目:高中数学 来源:2015届陕西省宝鸡市金台区高二下学期期末考试文科数学试卷(解析版) 题型:选择题
设函数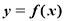 ,用二分法求方程
,用二分法求方程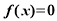 在
在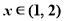 内近似解的过程中得
内近似解的过程中得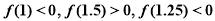 则方程的根落在区间 ( )
则方程的根落在区间 ( )
A.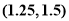 B.
B.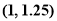 C.
C.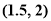 D.不能确定
D.不能确定
查看答案和解析>>
科目:高中数学 来源:2015届陕西省咸阳市高二下学期期末质量检测理科数学试卷(解析版) 题型:选择题
投掷两颗骰子,得到其向上的点数分别为m和n,则复数(m+ni)(n﹣mi)为实数的概率为( )
A. B.
B. C.
C.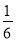 D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届陕西省咸阳市高二下学期期末质量检测文科数学试卷(解析版) 题型:选择题
下列命题中是全称命题的是( )
A.圆有内接四边形
B.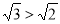
C.
D.若三角形的三边长分别为3、4、5,则这个三角形为直角三角形
查看答案和解析>>
科目:高中数学 来源:2015届重庆市高二下期期中考试理科数学试卷(解析版) 题型:选择题
如图:在平行六面体 中,
中, 为
为 与
与 的交点。若
的交点。若 ,
,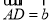 ,
, 则下列向量中与
则下列向量中与 相等的向量是( )
相等的向量是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届重庆市高二下期期中考试文科数学试卷(解析版) 题型:选择题
设双曲线 的两条渐近线与直线
的两条渐近线与直线 分别交于A,B两点,F为该双曲线的右焦点.若
分别交于A,B两点,F为该双曲线的右焦点.若 , 则该双曲线的离心率的取值范围是( )
, 则该双曲线的离心率的取值范围是( )
A. B.
B. C.
C.  D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com