
【题目】已知点![]() 在椭圆
在椭圆![]() :
: ![]() 上,
上, ![]() 是椭圆的一个焦点.
是椭圆的一个焦点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)椭圆C上不与![]() 点重合的两点
点重合的两点![]() ,
, ![]() 关于原点O对称,直线
关于原点O对称,直线![]() ,
, ![]() 分别交
分别交![]() 轴于
轴于![]() ,
, ![]() 两点.求证:以
两点.求证:以![]() 为直径的圆被直线
为直径的圆被直线![]() 截得的弦长是定值.
截得的弦长是定值.
【答案】(Ⅰ)![]() .(Ⅱ)见解析.
.(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)依题意,得到![]() ,利用定义得到
,利用定义得到![]() ,即可求解椭圆的标准方程;
,即可求解椭圆的标准方程;
(Ⅱ)设![]() ,
, ![]() ,根据直线方程,求解
,根据直线方程,求解![]() 的坐标,可得
的坐标,可得![]() ,利用
,利用 ![]() ,求得
,求得![]() 的值,即可得到弦长为定值.
的值,即可得到弦长为定值.
试题解析:
(Ⅰ)依题意,椭圆的另一个焦点为![]() ,且
,且![]() .
.
因为 ,
,
所以![]() ,
, ![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)证明:由题意可知![]() ,
, ![]() 两点与点
两点与点![]() 不重合.
不重合.
因为![]() ,
, ![]() 两点关于原点对称,
两点关于原点对称,
所以设![]() ,
, ![]() ,
, ![]() .
.
设以![]() 为直径的圆与直线
为直径的圆与直线![]() 交于
交于![]() 两点,
两点,
所以![]() .
.
直线![]() :
: 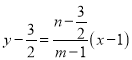 .
.
当![]() 时,
时,  ,所以
,所以 .
.
直线![]() :
: 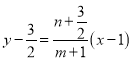 .
.
当![]() 时,
时, 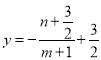 ,所以
,所以 .
.
所以 ,
, 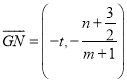 ,
,
因为![]() ,所以
,所以![]() ,
,
所以 .
.
因为![]() ,即
,即![]() ,
, ![]() ,
,
所以![]() ,所以
,所以![]() .
.
所以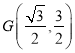 ,
, 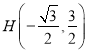 , 所以
, 所以![]() .
.
所以以![]() 为直径的圆被直线
为直径的圆被直线![]() 截得的弦长是定值
截得的弦长是定值![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() ,点
,点![]() 是线段
是线段![]() 的中点。
的中点。
(1)求直线![]() 的方程;
的方程;
(2)是否存在与直线![]() 平行的直线
平行的直线![]() ,使得
,使得![]() 与与圆
与与圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() 不经过点
不经过点![]() ,且
,且![]() 的面积
的面积![]() 最大?若存在,求出
最大?若存在,求出![]() 的方程及对应的
的方程及对应的![]() 的面积S;若不存在,请说明理由。
的面积S;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() :
: ![]() 上,
上, ![]() 是椭圆的一个焦点.
是椭圆的一个焦点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)椭圆C上不与![]() 点重合的两点
点重合的两点![]() ,
, ![]() 关于原点O对称,直线
关于原点O对称,直线![]() ,
, ![]() 分别交
分别交![]() 轴于
轴于![]() ,
, ![]() 两点.求证:以
两点.求证:以![]() 为直径的圆被直线
为直径的圆被直线![]() 截得的弦长是定值.
截得的弦长是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】济南新旧动能转换先行区,承载着济南从“大明湖时代”迈向“黄河时代”的梦想,肩负着山东省新旧动能转换先行先试的重任,是全国新旧动能转换的先行区.先行区将以“结构优化质量提升”为目标,通过开放平台汇聚创新要素,坚持绿色循环保障持续发展,建设现代绿色智慧新城.2019年某智能机器人制造企业有意落户先行区,对市场进行了可行性分析,如果全年固定成本共需2000(万元),每年生产机器人![]() (百个),需另投人成本
(百个),需另投人成本![]() (万元),且
(万元),且 ,由市场调研知,每个机器人售价6万元,且全年生产的机器人当年能全部销售完.
,由市场调研知,每个机器人售价6万元,且全年生产的机器人当年能全部销售完.
(1)求年利润![]() (万元)关于年产量
(万元)关于年产量![]() (百个)的函数关系式;(利润=销售额-成本)
(百个)的函数关系式;(利润=销售额-成本)
(2)该企业决定:当企业年最大利润超过2000(万元)时,才选择落户新旧动能转换先行区.请问该企业能否落户先行区,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益![]() 与投资额
与投资额![]() 成正比,且投资1万元时的收益为
成正比,且投资1万元时的收益为![]() 万元,投资股票等风险型产品的收益
万元,投资股票等风险型产品的收益![]() 与投资额
与投资额![]() 的算术平方根成正比,且投资1万元时的收益为0.5万元,
的算术平方根成正比,且投资1万元时的收益为0.5万元,
(1)分别写出两种产品的收益与投资额的函数关系;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎样分配资金能使投资获得最大收益,其最大收益为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目,若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.
某学校为了了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有8人 | 8 | 8 | 4 | 2 | 1 | 1 |
选考方案待确定的有6人 | 4 | 3 | 0 | 1 | 0 | 0 | |
女生 | 选考方案确定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 |
选考方案待确定的有6人 | 5 | 4 | 1 | 0 | 0 | 1 |
(Ⅰ)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?
(Ⅱ)假设男生、女生选择选考科目是相互独立的.从选考方案确定的8位男生随机选出1人,从选考方案确定的10位女生中随机选出1人,试求该男生和该女生的选考方案中都含有历史科目的概率;
(Ⅲ)从选考方案确定的8名男生随机选出2名,设随机变量两名男生选考方案相同时![]() ,两名男生选考方案不同时
,两名男生选考方案不同时![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,动圆
,动圆![]() 与圆
与圆![]() 内切且与圆
内切且与圆![]() 外切.
外切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知![]() 与
与![]() 为平面内的两个定点,过
为平面内的两个定点,过![]() 点的直线
点的直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com