
分析 令函数y=2xf(x)-3=0,得到方程f(x)=$\frac{3}{2x}$,从而化函数的零点为方程的根,再转化为两个函数的交点问题,然后逐一分区间求得答案.
解答 解:令函数y=2xf(x)-3=0,得到方程f(x)=$\frac{3}{2x}$,
当x∈[1,2)时,函数f(x)先增后减,在x=$\frac{3}{2}$时取得最大值1,
而y=$\frac{3}{2x}$在x=$\frac{3}{2}$时也有y=1;
当x∈[2,22)时,f(x)=$\frac{1}{2}$f($\frac{1}{2}$x),在x=3处函数f(x)取得最大值$\frac{1}{2}$,
而y=$\frac{3}{2x}$在x=3时也有y=$\frac{1}{2}$;
当x∈[22,23)时,f(x)=$\frac{1}{2}$f($\frac{1}{2}$x),在x=6处函数f(x)取得最大值$\frac{1}{4}$,
而y=$\frac{3}{2x}$在x=6时也有y=$\frac{1}{4}$;
…;
当x∈[210,211)时,f(x)=$\frac{1}{2}$f($\frac{1}{2}$x),在x=1536处函数f(x)取得最大值$\frac{1}{210}$,
而y=$\frac{3}{2x}$在x=1536时也有y=$\frac{1}{210}$.
∴函数y=2xf(x)-3在区间(1,2017)上的零点个数为11.
故答案为:11.
点评 本题考查了函数的零点与方程的根的关系及函数的交点的应用,体现了数学转化思想方法及分类讨论的数学思想方法,是压轴题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $-\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $-\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 羊毛颜色 | 每匹需要/kg | 供应量/kg | |
| 布料A | 布料B | ||
| 红 | 3 | 3 | 1050 |
| 绿 | 4 | 2 | 1200 |
| 黄 | 2 | 6 | 1800 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
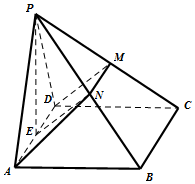 在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A、D、N三点的平面交PC于M,E为AD中点.
在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A、D、N三点的平面交PC于M,E为AD中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
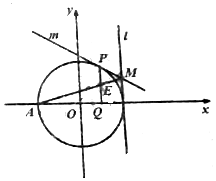 如图,点P是圆O:x2+y2=4上一点,圆O在点P处的切线为m,PQ垂直x轴于点Q(P、Q不重合),线段PQ的重点为E,点A(-2,0),直线l:x=2与直线m交于点M.
如图,点P是圆O:x2+y2=4上一点,圆O在点P处的切线为m,PQ垂直x轴于点Q(P、Q不重合),线段PQ的重点为E,点A(-2,0),直线l:x=2与直线m交于点M.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com