
在数列{an}中,an+1+an=2n-44(n∈N*),a1=-23.
(1)求an;
(2)设Sn为{an}的前n项和,求Sn的最小值.
思路分析 由已知条件可推知n应分奇数和偶数.
解析 (1)由an+1+an=2n-44(n∈N*),
an+2+an+1=2(n+1)-44.
∴an+2-an=2,又a2+a1=2-44,∴a2=-19.
同理得:a3=-21,a4=-17.故a1,a3,a5,…是以a1为首项、2为公差的等差数列,a2,a4,a6,…是以a2为首项、2为公差的等差数列.
从而an=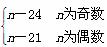
(2)当n为偶数时,
Sn=(a1+a2)+(a3+a4)+…+(an-1+an)
=(2×1-44)+(2×3-44)+…+[2×(n-1)-44]
=2[1+3+…+(n-1)]-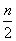 ·44=
·44=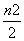 -22n,
-22n,
故当n=22时,Sn取得最小值-242.
当n为奇数时,
Sn=a1+(a2+a3)+(a4+a5)+…+(an-1+an)=a1+(2×2-44)+…+[2×(n-1)-44]
=a1+2[2+4+…+(n-1)]+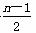 ·(-44)
·(-44)
=-23+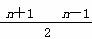 -22(n-1)
-22(n-1)
=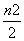 -22n-
-22n-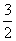 .
.
故当n=21或n=23时,Sn取得最小值-243.


科目:高中数学 来源: 题型:
已知数列{an}是首项为-1,公差d 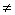 0的等差数列,且它的第2、3、6项依次构成等比数列{ bn}的前3项。
0的等差数列,且它的第2、3、6项依次构成等比数列{ bn}的前3项。
(1)求{an}的通项公式;
(2)若Cn=an·bn,求数列{Cn}的前n项和Sn。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com