Question

16．持续高温使漳州市多地出现气象干旱，城市用水紧张，为了宣传节约用水，某人准备在一片扇形区域（如图3）上按照图4的方式放置一块矩形ABCD区域宣传节约用水，其中顶点B，C在半径ON上，顶点A在半径OM上，顶点D在$\widehat{NM}$上，∠MON=$\frac{π}{6}$，ON=OM=10，m，设∠DON=θ，矩形ABCD的面积为S．

（Ⅰ）用含θ的式子表示DC，OB的长‘
（Ⅱ）若此人布置1m²的宣传区域需要花费40元，试将S表示为θ的函数，并求布置此矩形宣传栏最多要花费多少元钱？（精确到0.01）
（参考数据：$\sqrt{3}$≈1.732，$\sqrt{2}$≈1.414）

Answer 1

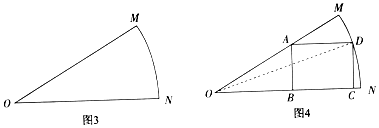
分析 （Ⅰ）直接在三角形中利用三角函数可以表示DC、OB的长；
（Ⅱ）S=BC×CD，求出相应函数，再利用导数方法研究函数的最大值．

解答 解：（Ⅰ）在△ODC中DC=10sinθ，在△OAB中，OB=10$\sqrt{3}$sinθ；
（Ⅱ）在△ODC中OC=10cosθ，从而S=BC×CD=100（cosθsinθ-$\sqrt{3}$sin²θ）（0＜θ＜$\frac{π}{6}$）
由S′=100（-sin²θ+cos²θ-2$\sqrt{3}$sinθcosθ）=0得tan2θ=$\frac{\sqrt{3}}{3}$，
由0＜θ＜$\frac{π}{6}$，得θ=$\frac{π}{12}$，易得θ=$\frac{π}{12}$时，S的最大值为100（1-$\frac{\sqrt{3}}{2}$）≈13.4．
此人布置1m²的宣传区域需要花费40元，
∴布置此矩形宣传栏最多要花费13.4×40=536元钱．

点评 解决实际问题的关键在于建立数学模型和目标函数，把“问题情境”译为数学语言，找出问题的主要关系，并把问题的主要关系抽象成数学问题，在数学领域寻找适当的方法解决，再返回到实际问题中加以说明．