
【题目】过抛物线![]() )的焦点F且斜率为1的直线交抛物线C于M,N两点,且
)的焦点F且斜率为1的直线交抛物线C于M,N两点,且![]() .
.
(1)求p的值;
(2)抛物线C上一点![]() ,直线
,直线![]() (其中
(其中![]() )与抛物线C交于A,B两个不同的点(A,B均与点Q不重合).设直线QA,QB的斜率分别为
)与抛物线C交于A,B两个不同的点(A,B均与点Q不重合).设直线QA,QB的斜率分别为![]() .
.
(i)直线l是否过定点?如果是,请求出所有定点;如果不是,请说明理由;
(ii)设点T在直线l上,且满足![]() ,其中
,其中![]() 为坐标原点.当线段
为坐标原点.当线段![]() 最长时,求直线l的方程.
最长时,求直线l的方程.
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,且
,且![]() 与短轴的一个端点Q构成一个等腰直角三角形,点P(
与短轴的一个端点Q构成一个等腰直角三角形,点P(![]() )在椭圆
)在椭圆![]() 上,过点
上,过点![]() 作互相垂直且与x轴不重合的两直线AB,CD分别交椭圆
作互相垂直且与x轴不重合的两直线AB,CD分别交椭圆![]() 于A,B,C,D且M,N分别是弦AB,CD的中点
于A,B,C,D且M,N分别是弦AB,CD的中点
(1)求椭圆的方程
(2)求证:直线MN过定点R(![]() )
)
(3)求![]() 面积的最大值
面积的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图因事故都受到不同程度的损坏,但可见部分如下,据此解答如下问题:
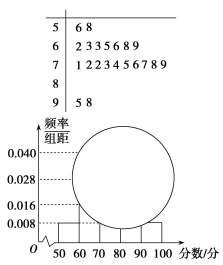
(1)求分数在[50,60)的频率及全班人数;
(2)求分数在[80,90)的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)若规定:90分(包含90分)以上为优秀,现从分数在80分(包含80分)以上的试卷中任取两份分析学生失分情况,求在抽取的试卷中至少有一份优秀的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:指数函数![]() 在R上是单调减函数;命题q:关于x的方程
在R上是单调减函数;命题q:关于x的方程![]() 有实根,
有实根,
(1)若p为真,求a的范围
(2)若q为真,求![]() 的范围
的范围
(3)若p或q为真,p且q为假,求实数a的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,若
,若![]() 为
为![]() 的中点.
的中点.

(1)证明:![]() 平面
平面![]() ;
;
(2)求异面直线![]() 和
和![]() 所成角;
所成角;
(3)设线段![]() 上有一点
上有一点![]() ,当
,当![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省确定从2021年开始,高考采用“![]() ”的模式,取消文理分科,即“3”包括语文、数学、外语,为必考科目;“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取
”的模式,取消文理分科,即“3”包括语文、数学、外语,为必考科目;“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取![]() 名学生进行调查.
名学生进行调查.
(1)已知抽取的![]() 名学生中含男生110人,求
名学生中含男生110人,求![]() 的值及抽取到的女生人数;
的值及抽取到的女生人数;
(2)学校计划在高二上学期开设选修中的“物理”和“历史”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的n名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目).下表是根据调查结果得到的![]() 列联表,请将列联表补充完整,并判断是否有99.5%的把握认为选择科目与性别有关?
列联表,请将列联表补充完整,并判断是否有99.5%的把握认为选择科目与性别有关?
说明你的理由;

(3)在(2)的条件下,从抽取的选择“物理”的学生中按分层抽样抽取6人,再从这6名学生中抽取2人,对“物理”的选课意向作深入了解,求2人中至少有1名女生的概率.
附:![]() ,其中
,其中![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-2ax-1+a,a∈R.
(1)若a=2,试求函数y=![]() (x>0)的最小值;
(x>0)的最小值;
(2)对于任意的x∈[0,2],不等式f(x)≤a成立,试求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科技公司新研制生产一种特殊疫苗,为确保疫苗质量,定期进行质量检验.某次检验中,从产品中随机抽取100件作为样本,测量产品质量体系中某项指标值,根据测量结果得到如下频率分布直方图:

(1)求频率分布直方图中![]() 的值;
的值;
(2)技术分析人员认为,本次测量的该产品的质量指标值X服从正态分布![]() ,若同组中的每个数据用该组区间的中间值代替,计算
,若同组中的每个数据用该组区间的中间值代替,计算![]() ,并计算测量数据落在(187.8,212.2)内的概率;
,并计算测量数据落在(187.8,212.2)内的概率;
(3)设生产成本为y元,质量指标值为![]() ,生产成本与质量指标值之间满足函数关系
,生产成本与质量指标值之间满足函数关系![]() 假设同组中的每个数据用该组区间的中间值代替,试计算生产该疫苗的平均成本.
假设同组中的每个数据用该组区间的中间值代替,试计算生产该疫苗的平均成本.
参考数据:![]() ,
,![]()
![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂利用辐射对食品进行灭菌消毒,现准备在该厂附近建一职工宿舍,并对宿舍进行防辐射处理,建房防辐射材料的选用与宿舍到工厂距离有关.若建造宿舍的所有费用p(万元)和宿舍与工厂的距离x(km)的关系为![]() ,若距离为1km时,测算宿舍建造费用为100万元.为了交通方便,工厂与宿舍之间还要修一条道路,已知购置修路设备需5万元,铺设路面每公里成本为6万元,设f(x)为建造宿舍与修路费用之和.
,若距离为1km时,测算宿舍建造费用为100万元.为了交通方便,工厂与宿舍之间还要修一条道路,已知购置修路设备需5万元,铺设路面每公里成本为6万元,设f(x)为建造宿舍与修路费用之和.
(1)求f(x)的表达式
(2)宿舍应建在离工厂多远处,可使总费用f(x)最小并求最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com