练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某颜料公司生产 两种产品，其中生产每吨产品，需要甲染料1吨，乙染料4吨，丙染料2吨，生产每吨产品，需要甲染料1吨，乙染料0吨，丙染料5吨，且该公司一条之内甲、乙、丙三种染料的用量分别不超过50吨，160吨和200吨，如果产品的利润为300元/吨， 产品的利润为200元/吨，则该颜料公司一天之内可获得最大利润为（ ）

    A. 14000元 B. 16000元 C. 18000元 D. 20000元

    【答案】A

    【解析】依题意，将题中数据统计如下表所示：

    设该公司一天内安排生产产品吨， 产品吨，所获利润为元.依据题意得目标函数为，约束条件为欲求目标函数的最大值，先画出约束条件表示的可行域，如图中阴影部分所示，则点， ， ， ， 作直线，当移动该直线过点时， 取得最大值，则也取得最大值（也可通过代入凸多边形端点进行计算，比较大小求得）.故，所以工厂每天生产产品40吨， 产品10吨时，才可获得最大利润，为14000元.选A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图几何体中，矩形所在平面与梯形所在平面垂直，且， ， ， 为的中点.

    （1）证明： 平面；

    （2）证明： 平面.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球，现从甲、乙两个盒子中各取出1个球，每个球被取出的可能性相等．
    （1）求取出的两个球上标号为相同数字的概率；
    （2）求取出的两个球上标号之积能被3整除的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于维向量，若对任意均有或，则称为维向量. 对于两个维向量定义.

    （1）若, 求的值；

    （2）现有一个维向量序列： 若且满足： ，求证：该序列中不存在维向量.

    (3) 现有一个维向量序列： 若且满足： ，若存在正整数使得为维向量序列中的项，求出所有的.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，设P是圆x2＋y2＝25上的动点，点D是P在x轴上的投影，M为PD上一点，且|MD|＝|PD|，当P在圆上运动时，求点M的轨迹C的方程。

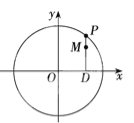
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足an+1= ，a1=1，n∈N* ．
    （1）求a2 ， a3 ， a4的值；
    （2）求数列{an}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校为了制定治理学校门口上学、放学期间家长接送孩子乱停车现象的措施，对全校学生家长进行了问卷调查，根据从其中随机抽取的50份调查问卷，得到了如下的列联表.

    同意限定区域停车

    不同意限定区域停车

    合计

    男

    18

    7

    25

    女

    12

    13

    25

    合计

    30

    20

    50

    （1）学校计划在同意限定区域停车的家长中，按照分层抽样的方法，随机抽取5人在上学、放学期间在学校门口参与维持秩序，在随机抽取的5人中，选出2人担任召集人，求至少有一名女性的概率？

    （2）已知在同意限定区域停车的12位女性家长中，有3位日常开车接送孩子，现从这12位女性家长中随机抽取3人参与维持秩序，记参与维持秩序的女性家长中，日常开车接送孩子的女性家长人数为，求 的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）=sin2（2x﹣ ）﹣2tsin（2x﹣ ）+t2﹣6t+1（x∈[ ， ]）其最小值为g（t）．
    （1）求g（t）的表达式；
    （2）当﹣ ≤t≤1时，要使关于t的方程g（t）=kt有一个实根，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为直角坐标系的坐标原点，双曲线 上有一点（），点在轴上的射影恰好是双曲线的右焦点，过点作双曲线两条渐近线的平行线，与两条渐近线的交点分别为， ，若平行四边形的面积为1，则双曲线的标准方程是（ ）

    A. B. C. D.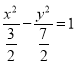

    查看答案和解析>>

    同步练习册答案