练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

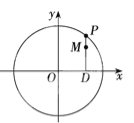
    【题目】如图，设P是圆x2＋y2＝25上的动点，点D是P在x轴上的投影，M为PD上一点，且|MD|＝|PD|，当P在圆上运动时，求点M的轨迹C的方程。

    【答案】

    【解析】

    试题分析：这是一道典型的关于轨迹问题的题目，通常的解法：①设出所求轨迹点的坐标；②找出已知点的坐标与其之间的等量关系；③代入已知点的轨迹方程；④求出所求点的轨迹方程.在此题的解答过程中，可以先设出所求点的坐标，已知点的坐标，由“点是在轴上的投影”且“”得到点与点坐标之间的等量关系，又由于点是已知圆上的点，将其坐标代入圆方程，经整理即可得到所点的轨迹方程.

    试题解析：设的坐标为，的坐标为，则由已知得 5分

    因为点在圆上，所以，即所求点的轨迹的方程为. 10分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在30瓶饮料中，有3瓶已过了保质期．从这30瓶饮料中任取2瓶，已知所取的2瓶全在保质期内的概率为 ，则至少取到1瓶已过保质期的概率为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线C：y2＝4x的焦点为F，过点F的直线l与C相交于A，B两点，若|AB|＝8，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数．

    （Ⅰ）当时，求曲线在点处的切线方程；

    （Ⅱ）设，若对任意的，存在使得成立，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆： 的短轴长为，右焦点为，点是椭圆上异于左、右顶点的一点．

    （1）求椭圆的方程；

    （2）若直线与直线交于点，线段的中点为，证明：点关于直线的对称点在直线上．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某颜料公司生产 两种产品，其中生产每吨产品，需要甲染料1吨，乙染料4吨，丙染料2吨，生产每吨产品，需要甲染料1吨，乙染料0吨，丙染料5吨，且该公司一条之内甲、乙、丙三种染料的用量分别不超过50吨，160吨和200吨，如果产品的利润为300元/吨， 产品的利润为200元/吨，则该颜料公司一天之内可获得最大利润为（ ）

    A. 14000元 B. 16000元 C. 18000元 D. 20000元

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数y=Asin（ωx+φ）在一个周期内的图象如图，此函数的解析式为（ ）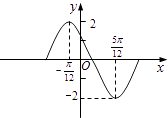

    A.y=2sin（2x+ ）
    B.y=2sin（2x+ ）
    C.y=2sin（ ﹣ ）
    D.y=2sin（2x﹣ ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=2sin（2x﹣ ），x∈R．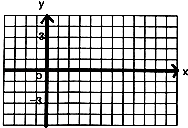

    （1）在给定的平面直角坐标系中，画函数f（x）=2sin（2x﹣ ），x∈[0，π]的简图；
    （2）求f（x）=2sin（2x﹣ ），x∈[﹣π，0]的单调增区间；
    （3）函数g（x）=2cos2x的图象只经过怎样的平移变换就可得到f（x）=2sin（2x﹣ ），x∈R的图象？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求在上的最大值和最小值；

    （2）设曲线与轴正半轴的交点为处的切线方程为,求证：对于任意的正实数，都有.

    查看答案和解析>>

    同步练习册答案