解:(I)由①知,对任意a,b∈N
*,a<b,都有(a-b)(f(a)-f(b))>0,
由于a-b<0,从而f(a)<f(b),
所以函数f(x)为N
*上的单调增函数.
(II)令f(1)=a,则a≥1,显然a≠1,否则f(f(1))=f(1)=1,与f(f(1))=3矛盾.
从而a>1,而由f(f(1))=3,
即得f(a)=3.
又由(I)知f(a)>f(1)=a,即a<3.
于是得1<a<3,又a∈N
*,
从而a=2,即f(1)=2.
进而由f(a)=3知,f(2)=3.
于是f(3)=f(f(2))=3×2=6,
(III)f(a
n)=f(f(3
n))=3×3
n=3
n+1,a
n+1=f(3
n+1)=f(f(a
n))=3a
n,a
1=f(3)=6.
即数列{a
n}是以6为首项,以3为公比的等比数列.
∴a
n=6×3
n-1=2×3
n(n=1,2,3).
于是
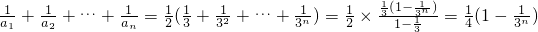
,
显然
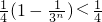
,
另一方面3
n=(1+2)
n=1+C
n1×2+C
n2×2
2+…+C
nn×2
n≥1+2n,
从而
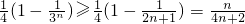
.
综上所述,
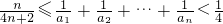
.
分析:(I)由已知条件中对任意a,b∈N
*,a≠b,我们不妨令a<b,则可将已知中af(a)+bf(b)>af(b)+bf(a)变形为(a-b)(f(a)-f(b))>0由a<b判断出f(a)-f(b)的符号,结合单调性的定义,即可作出结论.
(II)由对任意n∈N
*都有f[f(n)]=3n.我们不妨令f(1)=a,然后分a<1,a=1,a>1三类进行讨论,再由a∈N
*,可以求出a值,进而求得f(2),f(3)的值;
(III)a
n=f(3
n),则易得f(a
n)=f(f(3
n))=3×3
n=3
n+1,a
n+1=f(3
n+1)=f(f(a
n))=3a
n,a
1=f(3)=6.分析可知数列{a
n}是以6为首项,以3为公比的等比数列再利用放缩法可证明
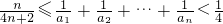
成立.
点评:(1)对于抽象函数的函数值的求法,我们不可能求出函数的解析式,但观察到af(a)+bf(b)>af(b)+bf(a)移项分解后的形式,故可据此分析函数的单调性;(2)中分类讨论求f(1)的值,及根据已知条件和(1)的结论得到f(28)值用到需要较强的逻辑能力;(3)中放缩法是证明不等式常用的方法,要求大家了解并学会使用.属中档题.

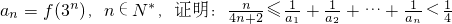 .
.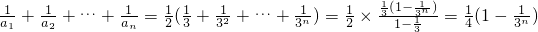 ,
,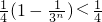 ,
,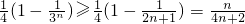 .
.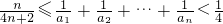 .
.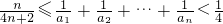 成立.
成立.

 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为