已知函数f(x)=lnx-ax+1,a∈R是常数.
(1)求函数y=f(x)的图象在点P(1,f(1))处的切线l的方程;
(2)证明函数y=f(x)(x≠1)的图象在直线l的下方;
(3)若函数y=f(x)有零点,求实数a的取值范围.
【答案】
分析:(1)已知f(x)=lnx-ax+1,对你进行求导,根据导数和斜率的关系,求出切线的方程;
(2)作F(x)=f(x)-(1-a)x=lnx-x+1,x>0,利用导数证得任意x>0且x≠1,F(x)<0,从而有f(x)<(1-a)x,即函数y=f(x)(x≠1)的图象在直线l的下方.
(3)令y=0,进行变形lnx=ax-1,即
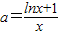
,令
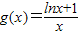
,利用导数的方法,研究其单调性及最大值,从而求出实数a的取值范围.
解答:解:(1)
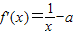
…(2分)f(1)=-a+1,k
l=f'(1)=1-a,
所以切线l的方程为y-f(1)=k
l(x-1),即y=(1-a)x.…(4分)
(2)令F(x)=f(x)-(1-a)x=lnx-x+1,x>0,
则
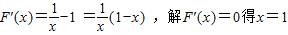
.
| x | (0,1) | 1 | (1,+∞) |
| F'(x) | + | | - |
| F(x) | ↗ | 最大值 | ↘ |
F(1)<0,所以?x>0且x≠1,F(x)<0,f(x)<(1-a)x,
即函数y=f(x)(x≠1)的图象在直线l的下方. …(9分)
(3)y=f(x)有零点,即f(x)=lnx-ax+1=0有解,
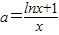
.
令
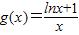
,
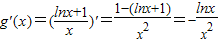
,
解g'(x)=0得x=1.…(11分)
则g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
当x=1时,g(x)的最大值为g(1)=1,
所以a≤1.…(13分)
点评:本题主要考查导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减,还考查了数形结合的思想,是一道中档题.

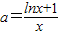 ,令
,令 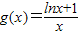 ,利用导数的方法,研究其单调性及最大值,从而求出实数a的取值范围.
,利用导数的方法,研究其单调性及最大值,从而求出实数a的取值范围.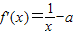 …(2分)f(1)=-a+1,kl=f'(1)=1-a,
…(2分)f(1)=-a+1,kl=f'(1)=1-a,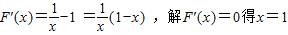 .
.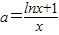 .
.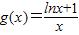 ,
,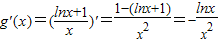 ,
,
