
若数列 中,
中, =1,
=1, ="3+5,"
="3+5,"  =7+9+11,
=7+9+11, =13+15+17+19,…,则
=13+15+17+19,…,则 = .
= .
1000
解析考点:归纳推理.
分析:观察数列{an} 中,各组和式的第一个数:1,3,7,13,…找出其规律,从而得出a10的第一个加数为91,最后再结合a10=91+93+…+91+2×9利用等差数列的求和公式即可得出答案.
解:观察数列{an} 中,a1=1,a2=3+5,a3=7+9+11,a4=13+15+17+19,…,
各组和式的第一个数为:1,3,7,13,…
即1,1+2,1+2+2×2,1+2+2×2+2×3,…,
其第n项为:1+2+2×2+2×3+…+2×(n-1).
∴第10项为:1+2+2×2+2×3+…+2×9=1+2×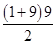 =91.
=91.
从而a10的第一个加数为91,
即a10=91+93+…+91+2×9=91×10+2×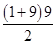 =1000.
=1000.
故答案为:1000.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 1 |
| anan+1 |
| 2012 |
| 2013 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com