
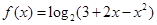 .
. 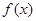 的定义域;
的定义域;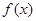 在
在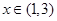 上是减函数;
上是减函数;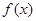 的值域.
的值域.科目:高中数学 来源:不详 题型:解答题
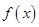 是定义在
是定义在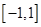 上的奇函数,且
上的奇函数,且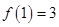 ,若
,若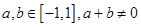 时,有
时,有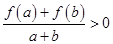 成立.
成立.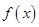 在
在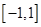 上的单调性,并证明;
上的单调性,并证明;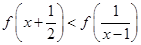 ;
;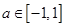 时,
时, 对所有的
对所有的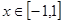 恒成立,求实数
恒成立,求实数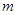 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
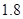 元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用(若
元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用(若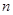 天购买一次,需要支付
天购买一次,需要支付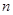 天的保管费)。其标准如下: 7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.
天的保管费)。其标准如下: 7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.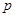 是多少元?[
是多少元?[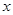 天购买一次配料,求该厂在这
天购买一次配料,求该厂在这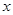 天中用于配料的总费用
天中用于配料的总费用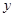 (元)关于
(元)关于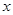 的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
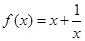 .
.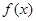 在
在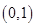 上是减函数;
上是减函数;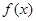 在
在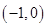 上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com