
���� ��1��$\overrightarrow{DA}$=$\overrightarrow{DC}+\overrightarrow{CB}+\overrightarrow{BA}$��$\overrightarrow{BC}$��$\overrightarrow{DA}$�������������߶������ɵó�����
��2��$\overrightarrow{AC}$=$\overrightarrow{AB}+\overrightarrow{BC}$=��2+x��-2+y����$\overrightarrow{BD}$=$\overrightarrow{BC}+\overrightarrow{CD}$=$��x+1��y+\frac{7}{2}��$����$\overrightarrow{AC}$��$\overrightarrow{BD}$���ɵ�$\overrightarrow{AC}$•$\overrightarrow{BD}$=0��������SABCD=$\frac{1}{2}|\overrightarrow{AC}||\overrightarrow{BD}|$���ɵó���
��� �⣺��1��$\overrightarrow{DA}$=$\overrightarrow{DC}+\overrightarrow{CB}+\overrightarrow{BA}$=-$��1��\frac{7}{2}��$-��x��y��-��2��-2��=��-3-x��-y-$\frac{3}{2}$����
��$\overrightarrow{BC}$��$\overrightarrow{DA}$����x��-y-$\frac{3}{2}$��-y��-3-x��=0����Ϊx=2y��
��2��$\overrightarrow{AC}$=$\overrightarrow{AB}+\overrightarrow{BC}$=��2+x��-2+y����$\overrightarrow{BD}$=$\overrightarrow{BC}+\overrightarrow{CD}$=$��x+1��y+\frac{7}{2}��$��
��$\overrightarrow{AC}$��$\overrightarrow{BD}$���ࣨ2+x����x+1��+��y-2����y+$\frac{7}{2}$��=0����x=2y��
�������$\left\{\begin{array}{l}{x=1}\\{y=\frac{1}{2}}\end{array}\right.$����$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$��
��$\overrightarrow{AC}$=$��3��-\frac{3}{2}��$��$\overrightarrow{BD}$=��2��4����$|\overrightarrow{AC}|$=$\frac{3\sqrt{5}}{2}$��$|\overrightarrow{BD}|$=$2\sqrt{5}$��
��$\overrightarrow{AC}$=��-2��-4����$\overrightarrow{BD}$=��-3��$\frac{3}{2}$����$|\overrightarrow{AC}|$=$2\sqrt{5}$��$|\overrightarrow{BD}|$=$\frac{3\sqrt{5}}{2}$��
��SABCD=$\frac{1}{2}|\overrightarrow{AC}||\overrightarrow{BD}|$=$\frac{1}{2}��2\sqrt{5}��\frac{3\sqrt{5}}{2}$=$\frac{15}{2}$��
���� ���⿼�����������߶�����������ֱ���������Ĺ��ߡ�����ģ�ļ��㹫ʽ��������������������������������е��⣮


 �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x+1��2+��y-1��2=6 | B�� | ��x-1��2+��y+1��2=6 | C�� | ��x+1��2+��y-1��2=3 | D�� | ��x-1��2+��y+1��2=3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��x��=lgx2��g��x��=2lgx | B�� | f��x��=$\sqrt{x+2}$•$\sqrt{x-2}$��g��x��=$\sqrt{��x+2����x-2��}$ | ||
| C�� | f��x��=x-2��g��x��=$\sqrt{��{x-2��}^{2}}$ | D�� | f��x��=lgx-2��g��x��=lg$\frac{x}{100}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
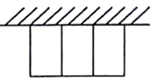 ��һ�����Ͽ��Խ���80m��Χǽ�����ô˲�����һ�߿�ǽ�ĵط�Χ��һ����γ��أ��м���ͬ���IJ��ϸ������������ȵ�С���Σ���ͼ��ʾ������Χǽ��Ȳ��ƣ���Χ�ɵľ��ε�������Ϊ��������
��һ�����Ͽ��Խ���80m��Χǽ�����ô˲�����һ�߿�ǽ�ĵط�Χ��һ����γ��أ��м���ͬ���IJ��ϸ������������ȵ�С���Σ���ͼ��ʾ������Χǽ��Ȳ��ƣ���Χ�ɵľ��ε�������Ϊ��������| A�� | 200m2 | B�� | 360m2 | C�� | 400m2 | D�� | 480m2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com