
【题目】已知函数![]() .
.
(1)当![]() 时,判断
时,判断![]() 的单调性;
的单调性;
(2)若![]() 在
在![]() 上为单调增函数,求实数
上为单调增函数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)在![]() 上为增函数;(2)
上为增函数;(2)![]() .
.
【解析】试题分析:(1)当![]() 时,对函数求导后因式分解,根据导数与单调性的知识可写出函数的单调区间.(2)当
时,对函数求导后因式分解,根据导数与单调性的知识可写出函数的单调区间.(2)当![]() 时,可判断函数导数恒为非负数,函数递增符合题意.当
时,可判断函数导数恒为非负数,函数递增符合题意.当![]() 和
和![]() 时,利用函数的二阶导数判断出不符合题意.故
时,利用函数的二阶导数判断出不符合题意.故![]() .
.
试题解析:
(1)当![]() 时,
时, 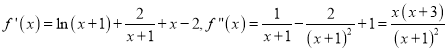 ,所以
,所以![]() 在
在![]() 上为减函数,在
上为减函数,在 ![]() 上为增函数,即
上为增函数,即![]() ,从而可得:
,从而可得: ![]() 在定义域
在定义域 ![]() 上为增函数.
上为增函数.
(2) ①当![]() 时,由于
时,由于![]() ,所以满足
,所以满足![]() 在
在 ![]() 上为单调增函数,即
上为单调增函数,即![]() ;
;
②当![]() 时,
时, ![]()
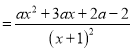 ,由方程
,由方程![]() 的判别式:
的判别式: ![]() ,所以方程有两根
,所以方程有两根![]() ,且由
,且由![]() 知
知![]() ,
, ![]() 在
在![]() 上为减函数,由
上为减函数,由![]() 可知,在
可知,在![]() 时,
时, ![]() ,这与
,这与 ![]() 在
在![]() 上为单调增函数相矛盾. ③ 当
上为单调增函数相矛盾. ③ 当![]() 时,
时, ![]()
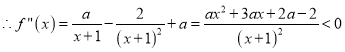 ,
, ![]() 在
在![]() 上为减函数,由
上为减函数,由![]() 可知,在
可知,在![]() 时,
时, ![]() ,这与
,这与 ![]() 在
在![]() 上为单调增函数也是相矛盾. 综上所述:实数
上为单调增函数也是相矛盾. 综上所述:实数![]() 的取值范围是
的取值范围是![]() .
.


 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
【题目】某社区超市购进了A,B,C,D四种新产品,为了解新产品的销售情况,该超市随机调查了15位顾客(记为![]() )购买这四种新产品的情况,记录如下(单位:件):
)购买这四种新产品的情况,记录如下(单位:件):
顾 客 产 品 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A | 1 | 1 | 1 | 1 | 1 | ||||||||||
B | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||
C | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||
D | 1 | 1 | 1 | 1 | 1 | 1 |
(Ⅰ)若该超市每天的客流量约为300人次,一个月按30天计算,试估计产品A的月销售量(单位:件);
(Ⅱ)为推广新产品,超市向购买两种以上(含两种)新产品的顾客赠送2元电子红包.现有甲、乙、丙三人在该超市购物,记他们获得的电子红包的总金额为X,
求随机变量X的分布列和数学期望;
(Ⅲ)若某顾客已选中产品B,为提高超市销售业绩,应该向其推荐哪种新产品?(结果不需要证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() ,离心率
,离心率![]() ,它的长轴长等于圆
,它的长轴长等于圆![]() 的直径.
的直径.
(1)求椭圆 ![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,是否存在定点
两点,是否存在定点![]() ,使得以
,使得以![]() 为直径的圆经过这个定点,若存在,求出定点
为直径的圆经过这个定点,若存在,求出定点![]() 的坐标;若不存在,请说明理由?
的坐标;若不存在,请说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中, ![]() ,顶点
,顶点![]() 在底面
在底面 ![]() 上的射影恰为点
上的射影恰为点 ![]() ,且
,且![]() .
.

(1)求棱 ![]() 与
与![]() 所成的角的大小;
所成的角的大小;
(2)在棱 ![]() 上确定一点
上确定一点![]() ,使
,使![]() ,并求出二面角
,并求出二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面![]() 平面
平面![]() ,
, ![]() 直线
直线![]() ,
, ![]() 是
是![]() 内不同的两点,
内不同的两点, ![]() 是
是![]() 内不同的两点,且
内不同的两点,且![]() 直线
直线![]() 上
上![]() 分别是线段
分别是线段![]() 的中点,下列判断正确的是( )
的中点,下列判断正确的是( )
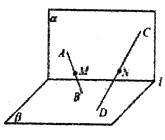
A. 当![]() 时,
时, ![]() 两点不可能重合
两点不可能重合
B. ![]() 两点可能重合,但此时直线
两点可能重合,但此时直线![]() 与
与![]() 不可能相交
不可能相交
C. 当![]() 与
与![]() 相交,直线
相交,直线![]() 平行于
平行于![]() 时,直线
时,直线![]() 可以与
可以与![]() 相交
相交
D. 当![]() 是异面直线时,直线
是异面直线时,直线![]() 可能与
可能与![]() 平行
平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是![]() .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: 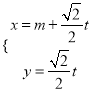 (
(![]() 是参数).
是参数).
(Ⅰ)将曲线C的极坐标方程化为直角坐标方程,将直线![]() 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)若直线l与曲线C相交于A、B两点,且![]() ,试求实数m的值.
,试求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com