
 ,
, ,
, 的最小值为
的最小值为 .
. 的解析式;
的解析式; ,若
,若 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;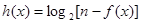 ,若此函数在定义域范围内不存在零点,求实数
,若此函数在定义域范围内不存在零点,求实数 的取值范围.[
的取值范围.[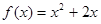 ;(2)
;(2)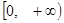 ;(3)
;(3)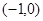 。
。  可设
可设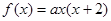 ,再由
,再由 的最小值
的最小值 求a的值;(2)首先对
求a的值;(2)首先对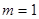 、
、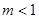 、
、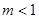 三种情况讨论,然后确定对称轴
三种情况讨论,然后确定对称轴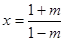 与给定区间
与给定区间 端点的关系;(3)要满足题意,须有
端点的关系;(3)要满足题意,须有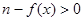 有解,且
有解,且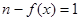 无解.然后求
无解.然后求 的最小值,令
的最小值,令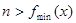 ,但
,但 不属于
不属于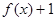 的值域,即可得实数
的值域,即可得实数 的取值范围。
的取值范围。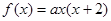 ,
, 的最小值为
的最小值为 , ∴
, ∴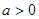 ,且
,且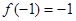 , ∴
, ∴ 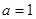 ,
,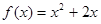 .
.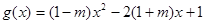 ,
,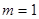 时,
时,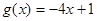 在[-1, 1]上是减函数,∴
在[-1, 1]上是减函数,∴ 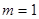 符合题意.
符合题意.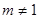 时,对称轴方程为:
时,对称轴方程为: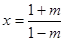 ,
,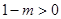 ,即
,即 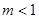 时,抛物线开口向上,
时,抛物线开口向上,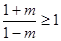 , 得
, 得 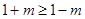 , ∴
, ∴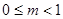 ;
;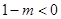 , 即
, 即 时,抛物线开口向下,
时,抛物线开口向下,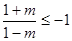 ,得
,得 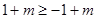 , ∴
, ∴ .
. 的取值范围为
的取值范围为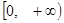 .
.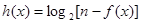 在定义域内不存在零点,必须且只须有
在定义域内不存在零点,必须且只须有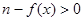 有解,且
有解,且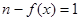 无解.
无解.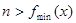 ,且
,且 不属于
不属于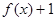 的值域,
的值域,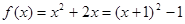 ,
, 的最小值为
的最小值为 ,
,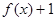 的值域为
的值域为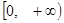 ,
,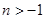 ,且
,且
 的取值范围为
的取值范围为 .
.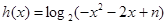 ,令
,令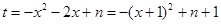 ,
,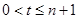 ,得
,得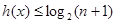 ,
,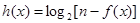 在定义域内不存在零点,
在定义域内不存在零点,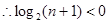 ,
,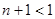 ,即
,即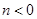 ,又
,又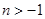 (否则函数定义域为空集,不是函数),
(否则函数定义域为空集,不是函数),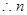 的取值范围是
的取值范围是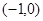 。
。

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源:不详 题型:解答题
 )的围墙,且要求中间用围墙
)的围墙,且要求中间用围墙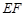 隔开,使得
隔开,使得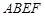 为矩形,
为矩形,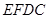 为正方形,设
为正方形,设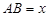 米,已知围墙(包括
米,已知围墙(包括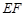 )的修建费用均为800元每米,设围墙(包括
)的修建费用均为800元每米,设围墙(包括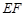 )的修建总费用为
)的修建总费用为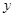 元。
元。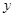 关于
关于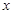 的函数解析式;
的函数解析式;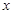 为何值时,设围墙(包括
为何值时,设围墙(包括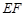 )的的修建总费用
)的的修建总费用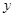 最小?并求出
最小?并求出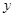 的最小值。
的最小值。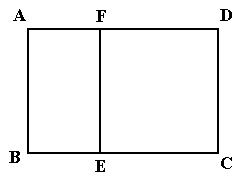
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
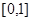 的函数
的函数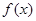 同时满足以下三个条件:
同时满足以下三个条件: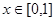 ,总有
,总有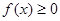 ;
;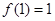 ;
; 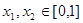 ,且
,且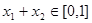 时,
时,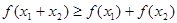 成立.
成立.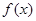 为“友谊函数”,求
为“友谊函数”,求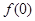 的值;
的值;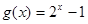 在区间
在区间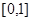 上是否为“友谊函数”?请给出理由;
上是否为“友谊函数”?请给出理由;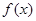 为“友谊函数”,假定存在
为“友谊函数”,假定存在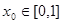 ,使得
,使得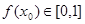 ,且
,且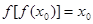 ,求证:
,求证: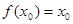 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| a | b | c | d | e | f | g | h | i | j | k | l | m |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| n | o | p | q | r | s | t | u | v | w | x | y | z |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
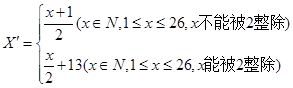
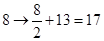 ,即
,即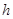 变成
变成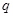 ;如
;如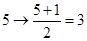 ,即
,即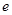 变成
变成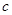 .
. 译成的密文是什么?
译成的密文是什么?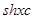 ,那么原来的明文是什么?
,那么原来的明文是什么?查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 =m?
=m? +n(其中O为坐标原点),若向量m=(
+n(其中O为坐标原点),若向量m=( ,3),n=(
,3),n=( ,0),则y=f(x)的最大值为________.
,0),则y=f(x)的最大值为________.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
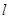 与曲线
与曲线 满足下列两个条件:
满足下列两个条件: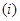 直线
直线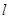 在点
在点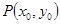 处与曲线
处与曲线 相切;
相切; 曲线
曲线 在
在 附近位于直线
附近位于直线 的两侧,则称直线
的两侧,则称直线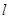 在点
在点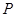 处“切过”曲线
处“切过”曲线 .
.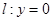 在点
在点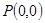 处“切过”曲线
处“切过”曲线 :
: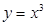
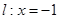 在点
在点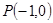 处“切过”曲线
处“切过”曲线 :
: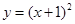
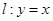 在点
在点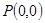 处“切过”曲线
处“切过”曲线 :
: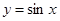
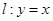 在点
在点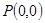 处“切过”曲线
处“切过”曲线 :
: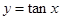
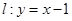 在点
在点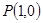 处“切过”曲线
处“切过”曲线 :
: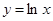
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com