分析:(1)对于确定性问题,我们可以使用反证明来进行证明,假设△B1MN是直角三角形,然后根据正方体的几何特征,及线面垂直的判定及性质我们易得到△B1MN中会出现两个直角,从而得到矛盾,进而得到原结论△B1MN不可能是直角三角形;
(2)连接MN,设MN∩BD=Q,(ⅰ)由正方形的几何性质,我们易得AC⊥BD,MN⊥BD,则DD1⊥面ABCD,再由DD1⊥MN,结合线面垂直的判定定理,即可得到平面B1MN⊥平面BB1D1D;(ⅱ)连接PM,PN,由B1D∥面PMN,由线面平行的性质,我们易得BD1∥PQ,然后根据平行线分线段成比例定理,得到B1P与PB的比值.
解答:解:(1)用反证法.如果△B
1MN是直角三角形,
不妨设
∠B1MN=,则MN⊥B
1M,(1分)
而B
1B⊥面ABCD,MN?面ABCD,∴B
1B⊥MN,B
1B∩B
1M=B
1,∴MN⊥面ABB
1A
1,∵AB?面ABB
1A
1,(2分)∴MN⊥AB,即
∠BMN=,与
∠MBN=矛盾!(3分)∴△B
1MN不可能是直角三角形.(4分)
(2)连接MN,设MN∩BD=Q则MN∥AC(5分)
∴AC⊥BD,MN⊥BD(7分)
又∵DD
1⊥面ABCD∴DD
1⊥MN
∴平面B
1MN⊥面BDD
1(9分)
(3)连接PM,PN则面PMN∩面BDD
1=PQ(10分)
当BD
1∥PQ时,BD
1∥面PMN(11分)
又M,N分别是AB,BC中点
=;
==.
点评:本题考查的知识点是平面与平面垂直的判定、三角形的形状判断,直线与平面平行的判定及反证法,掌握正方体的几何特征,及空间线面垂直、平行的判定、性质是解答本题的关键.

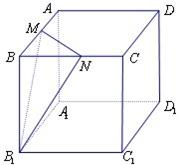 在正方体ABCD-A1B1C1D1中,M,N分别是棱AB,BC上异于端点的点,
在正方体ABCD-A1B1C1D1中,M,N分别是棱AB,BC上异于端点的点,

 16、在正方体ABCD-A′B′C′D′中,过对角线BD′的一个平面交AA′于E,交CC′于F,则
16、在正方体ABCD-A′B′C′D′中,过对角线BD′的一个平面交AA′于E,交CC′于F,则 如图,在正方体ABCD-A′B′C′D′中,E,F分别是AB′,BC′的中点.
如图,在正方体ABCD-A′B′C′D′中,E,F分别是AB′,BC′的中点.