Question

等差数列{a_n}中，a₁₀＜0，a₁₁＞0且a₁₁＞|a₁₀|，S_n为其前n项和，则（ ）
A．S₁，S₂，…，S₁₀都小于0，S₁₁，S₁₂，…都大于0
B．S₁，S₂，…，S₁₉都小于0，S₂₀，S₂₁，…都大于0
C．S₁，S₂，…，S₅都小于0，S₆，S₇，…都大于0
D．S₁，S₂，…，S₂₀都小于0，S₂₁，S₂₂，…都大于0

Answer 1

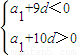
【答案】分析：先根据a₁₀＜0，a₁₁＞0可得到，故有d＞0，a₁＜0成立，结合a₁₁＞|a₁₀|可知a₁₀+a₁₁＞0，再由等差数列的性质可得到a₁+a₂₀=a₁₀+a₁₁＞0进而可得到S₂₀=10（a₁+a₂₀）＞0得到答案．
解答：解：由题意知
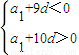
可得d＞0，a₁＜0．
又a₁₁＞|a₁₀|=-a₁₀，
∴a₁₀+a₁₁＞0．
由等差数列的性质知a₁+a₂₀=a₁₀+a₁₁＞0，
∴S₂₀=10（a₁+a₂₀）＞0．
故选B．
点评：本题主要考查等差数列的性质．考查基础知识的灵活运用．