
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
甲:对于x∈R,都有f(1+x)=f(1-x);
乙:在(-∞,0]上函数递减;
丙:在(0,+∞)上函数递增;
丁:f(0)不是函数的最小值.
如果其中恰有三人说得正确,请写出一个这样的函数:________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
甲:对于x∈R,都有f(1+x)=f(1-x);
乙:在(-∞,0]上函数递减;
丙:在(0,+∞)上函数递增;
丁:f(0)不是函数的最小值.
如果其中恰有三人说得正确,请写出一个这样的函数________________.
查看答案和解析>>
科目:高中数学 来源:2010年浙江省高一上学期10月月考数学卷 题型:填空题
老师给出一个函数,请三位同学各说出了这个函数的一条性质:
①此函数为偶函数;
②定义域为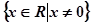 ;
;
③在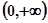 上为增函数.
上为增函数.
老师评价说其中有一个同学的结论错误,另两位同学的结论正确。请你写出一个(或几个)这样的函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com