练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图,已知正方体ABCD—A1B1C1D1中,E、F分别是AB和BC的中点,试问在棱DD1上能否找到一点M,使BM⊥平面B1EF?若能,试确定点M的位置;若不能,说明理由.

    解析:我们考虑如果BM⊥平面B1EF时,点M应该满足使BM⊥B1E,即其在平面A1B上的射影BP应该满足BP⊥B1E,经计算,不难得到点M应为DD1的中点.

    证明:如图,取DD1的中点M,AA1的中点P,CC1的中点Q.

        连结MP、MQ、BP、BQ,易证得MP⊥面ABB1A1,

    ∴MP⊥B1E.

        又由平面几何知BP⊥B1E,

    ∴B1E⊥平面MBP.

    ∴B1E⊥MB.

        同理可得BM⊥B1F.

        又B1E∩B1F=B1,

    ∴BM⊥平面B1EF.

    点评:证线面垂直常用的方法有:

    (1)利用定义,证明直线垂直于平面内的两条相交直线;

    (2)运用线面垂直的性质定理:两条平行直线中的一条垂直于一个平面,则另一条也垂直于这个平面.

        上述结论“BP⊥B1E”的证明可以为：Rt△ABP≌Rt△BB1E,进一步可推得BP⊥B1E.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    8、如图，已知正方体ABCD-A1B1C1D1的棱长为3，点E，F在线段AB上，点M在线段B1C1上，点N在线段C1D1上，且EF=1，D1N=x，AE=y，M是B1C1的中点，则四面体MNEF的体积（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

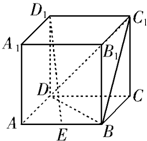    精英家教网如图，已知正方体ABCD-A1B1C1D1的棱长为2，点E为棱AB的中点．
    求：
    （1）D1E与平面BC1D所成角的正弦值；
    （2）二面角D-BC1-C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，已知正方体ABCD-A1B1C1D1的棱长为2，E、F分别是D1C、AB的中点．
    （I）求证：EF∥平面ADD1A1；
    （Ⅱ）求二面角D-EF-A的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，已知正方体ABCD-A1B1C1D1的棱长为2，点P，Q，R分别是棱AB，CC1，D1A1的中点．
    （1）求证：B1D⊥平面PQR；
    （2）设二面角B1-PR-Q的大小为θ，求|cosθ|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•宝山区一模）如图，已知正方体ABCD-A1B1C1D1 的棱长为2，E，F分别是BB1，CD的中点．
    （1）求三棱锥E-AA1F的体积；
    （2）求异面直线EF与AB所成角的大小（结果用反三角函数值表示）．

    查看答案和解析>>

    同步练习册答案