
分析 (1)由an+1=3an-1(n∈N*),可得an+1-$\frac{1}{2}$=3(an-$\frac{1}{2}$),利用等比数列的通项公式与求和公式即可得出.
(2)不等式$\frac{{a}_{n}+\frac{1}{2}}{{a}_{n+1}-\frac{3}{2}}$≤m,化为:$\frac{{3}^{n}+1}{{3}^{n+1}-1}$≤m,由于$\frac{{3}^{n}+1}{{3}^{n+1}-1}$=$\frac{1}{3}(1+\frac{4}{{3}^{n+1}-1})$单调递减,即可得出m的求值范围.
解答 解:(1)∵an+1=3an-1(n∈N*),∴an+1-$\frac{1}{2}$=3(an-$\frac{1}{2}$),
∴数列$\{{a}_{n}-\frac{1}{2}\}$是等比数列,首项为3,公比为3.
∴an-$\frac{1}{2}$=3×3n-1=3n,
∴an=$\frac{1}{2}$+3n,
∴Sn=$\frac{n}{2}$+$\frac{3({3}^{n}-1)}{3-1}$=$\frac{n+{3}^{n+1}-3}{2}$.
(2)不等式$\frac{{a}_{n}+\frac{1}{2}}{{a}_{n+1}-\frac{3}{2}}$≤m,化为:$\frac{{3}^{n}+1}{{3}^{n+1}-1}$≤m,
∵$\frac{{3}^{n}+1}{{3}^{n+1}-1}$=$\frac{1}{3}(1+\frac{4}{{3}^{n+1}-1})$单调递减,
∴m≥$\frac{1}{3}(1+\frac{4}{{3}^{2}-1})$=$\frac{1}{2}$.
∴实数m的取值范围是$[\frac{1}{2},+∞)$.
点评 本题考查了等比数列的通项公式与求和公式、数列的单调性,考查了推理能力与计算能力,属于中档题.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:填空题
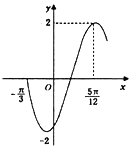 函数$f(x)=2sin({ωx+φ})({ω>0,-\frac{π}{2}<ω<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为y=2sin2x.
函数$f(x)=2sin({ωx+φ})({ω>0,-\frac{π}{2}<ω<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为y=2sin2x.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | (-∞,0) | B. | (4,+∞) | C. | (-∞,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 300只 | B. | 400只 | C. | 600只 | D. | 700只 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
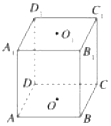 如图所示,在正方体ABCD-A1B1C1D1中,O1、O为上、下底面的中心,在直线D1D、A1D、A1D1、C1D1、O1D与平面AB1C平行的直线有2条.
如图所示,在正方体ABCD-A1B1C1D1中,O1、O为上、下底面的中心,在直线D1D、A1D、A1D1、C1D1、O1D与平面AB1C平行的直线有2条.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在如图所示的几何体中,四边形DCFE为正方形,四边形ABCD为等腰梯形,AB∥CD,AC=$\sqrt{3}$,AB=2BC=2,且AC⊥FB.
在如图所示的几何体中,四边形DCFE为正方形,四边形ABCD为等腰梯形,AB∥CD,AC=$\sqrt{3}$,AB=2BC=2,且AC⊥FB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com