
(10分)如图,已知AB是⊙O的直径,CD是⊙O的切线,C为切点,连接AC,过点A作AD⊥CD于点D,交⊙O于点E.

(Ⅰ)证明:∠AOC=2∠ACD;(Ⅱ)证明:ABCD=ACCE.
详见解析.
【解析】
试题分析:(Ⅰ)连结BC,∵CD是⊙O的切线,C为切点,由弦切角定理知∠ACD=∠ABC,
因为∠AOC是三角形OBC的外角,要证∠AOC=2∠ACD,只要证∠OCB=∠ABC;
(Ⅱ)要证ABCD=ACCE,只需证 ,只要证Rt△ABC∽Rt△CED,所以只要利用圆周角和弦切角证明∠OAC=∠OCA=∠CAE=∠ECD即可.
,只要证Rt△ABC∽Rt△CED,所以只要利用圆周角和弦切角证明∠OAC=∠OCA=∠CAE=∠ECD即可.
试题解析: 证明:(Ⅰ)连结BC,∵CD是⊙O的切线,C为切点,
∴∠ACD=∠ABC,
∵OB=OC,∴∠OCB=∠ABC,
又∵∠AOC=∠OCB+∠OBC,
∴∠AOC=2∠AC D.
(Ⅱ)∵AB是⊙O的直径,∴∠ACB=90°,
又∵AD⊥CD于D,∴∠ADC=90°,
∵CD是⊙O的切线,C为切点,OC为半径,
∴∠OAC=∠CAE,且OC⊥CD,
∴OC∥AD,又∵OC=OA,
∴∠OAC=∠OCA=∠CAE=∠ECD,
∴Rt△ABC∽Rt△CED,∴ ,
,
∴ABCD=ACCE.
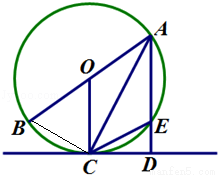
考点:1、圆周角;2、弦切角.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源:2014-2015学年河南省濮阳市高三上学期期末摸底考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知椭圆 长轴的端点为
长轴的端点为 、
、 ,且椭圆上的点到焦点的最小距离是
,且椭圆上的点到焦点的最小距离是 .
.
(1)求椭圆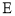 的标准方程;
的标准方程;
(2) 为原点,
为原点,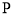 是椭圆
是椭圆 上异于
上异于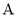 、
、 的任意一点,直线
的任意一点,直线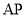 ,
, 分别交
分别交 轴于
轴于 ,
, ,问
,问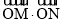 是否为定值,说明理由.
是否为定值,说明理由.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底文科数学试卷(解析版) 题型:选择题
已知函数f(x)=x3+ax2﹣9x+1,下列结论中错误的是( )
A.x0∈R,f(x0)=0
B.“a=3”是“﹣3为f(x)的极大值点”的充分不必要条件
C.若x0是f(x)的极小值点,则f(x)在区间(x0,+∞)单调递增
D.若3是f(x)的极值点,则f(x)的单调递减区间是(﹣1,3)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底文科数学试卷(解析版) 题型:选择题
设向量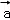 ,
, 满足|
满足| +
+ |=
|=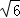 ,|
,| |=1,|
|=1,| |=2,则
|=2,则
 等于( )
等于( )
A. B.
B.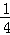 C.
C.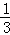 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底理科数学试卷(解析版) 题型:解答题
(10分)设数列{an}是公比为正数的等比数列,a1=2,a3﹣a2=12.
(1)求数列{an}的通项公式;
(2)设数列{bn}是首项为1,公差为2的等差数列,求数列{an+bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底理科数学试卷(解析版) 题型:选择题
已知函数f(x)=x3+ax2﹣9x+1,下列结论中错误的是( )
A.x0∈R,f(x0)=0
B.“a=3”是“﹣3为f(x)的极大值点”的充分不必要条件
C.若x0是f(x)的极小值点,则f(x)在区间(x0,+∞)单调递增
D.若3是f(x)的极值点,则f(x)的单调递减区间是(﹣1,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com