
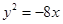 ,动圆恒过点(-2,0)则下列哪条直线是动圆的公切线()
,动圆恒过点(-2,0)则下列哪条直线是动圆的公切线()| A.x=4 | B.y=4 | C.x=2 | D.x=-2 |
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源:不详 题型:解答题
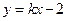 与抛物线C:
与抛物线C: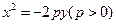 交于A,B两点,
交于A,B两点,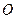 为坐标原点,
为坐标原点,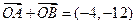 。
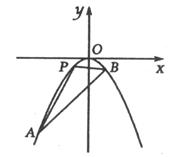
。
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
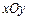 中的抛物线
中的抛物线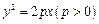 的焦点
的焦点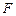 作一条倾斜角为
作一条倾斜角为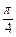 的直线与抛物线相交于A、B两点.
的直线与抛物线相交于A、B两点.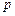 表示A、B之间的距离;
表示A、B之间的距离;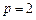 时,求
时,求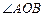 的余弦值.
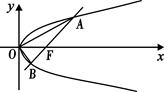
的余弦值.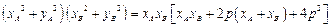 .
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
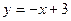 与
与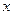 轴、
轴、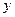 轴分别交于
轴分别交于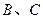 ,抛物线
,抛物线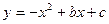 经过点
经过点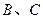 ,点
,点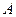 是抛物线与
是抛物线与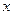 轴的另一个交点。
轴的另一个交点。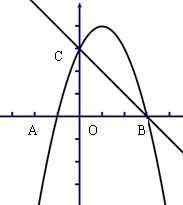
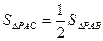 ,求P点坐标。
,求P点坐标。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
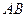 ⊥
⊥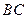 ,
,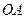 ∥
∥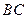 ,且
,且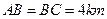 ,
,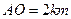 ,
, 曲线段
曲线段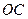 是以点
是以点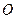 为顶
为顶 点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落
点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落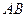 ,
,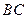 上,且一个顶点落在曲线段
上,且一个顶点落在曲线段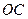 上.问:应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到
上.问:应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到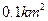 ).
).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com