
已知函数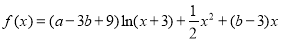 .
.
(1)当 且
且 ,
,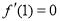 时,试用含
时,试用含 的式子表示
的式子表示 ,并讨论
,并讨论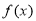 的单调区间;
的单调区间;
(2)若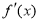 有零点,
有零点,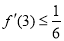 ,且对函数定义域内一切满足
,且对函数定义域内一切满足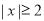 的实数
的实数 有
有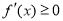 .
.
①求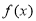 的表达式;
的表达式;
②当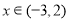 时,求函数
时,求函数 的图像与函数
的图像与函数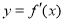 的图像的交点坐标.
的图像的交点坐标.
(1)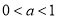 时,
时, 的单调增区间是
的单调增区间是 ,
,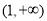 ,
, 单调减区间是
单调减区间是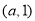 ;
;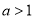 时,
时,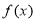 的单调增区间
的单调增区间 ,
, ,单调减区间为
,单调减区间为 ;
;
(2)① ;②
;② .
.
【解析】
试题分析:(1)先求出导函数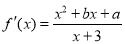 ,进而由
,进而由 ,于是
,于是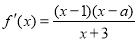 ,针对
,针对 分
分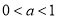 、
、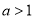 两种情况,分别求出
两种情况,分别求出 、
、 的解即可确定函数的单调区间;(2)①先由条件
的解即可确定函数的单调区间;(2)①先由条件 得到
得到 的一个不等关系式
的一个不等关系式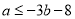 ,再由
,再由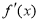 有零点,且对函数定义域内一切满足
有零点,且对函数定义域内一切满足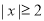 的实数
的实数 有
有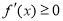 ,作出判断
,作出判断 的零点在
的零点在 内,设
内,设 ,则可得条件
,则可得条件 即
即 ,结合
,结合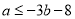 即可确定
即可确定 的取值,进而可写出
的取值,进而可写出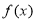 的解析式;②设
的解析式;②设 ,先通过函数的导数确定函数在
,先通过函数的导数确定函数在 的单调性,进而求出
的单调性,进而求出 在
在 的零点,进而即可求出
的零点,进而即可求出 与
与 的图像在区间
的图像在区间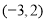 上的交点坐标.
上的交点坐标.
(1)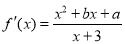
 2分
2分
由 ,故
,故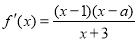
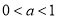 时,由
时,由 得
得 的单调增区间是
的单调增区间是 ,
,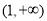
由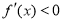 得
得 单调减区间是
单调减区间是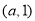
同理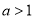 时,
时,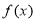 的单调增区间
的单调增区间 ,
, ,单调减区间为
,单调减区间为 5分
5分
(2)①由(1)及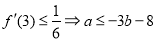 (i)
(i)
又由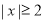
 有
有 知
知 的零点在
的零点在 内,设
内,设 ,
,
则 即
即
所以由条件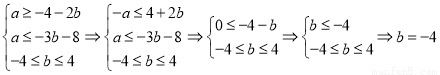
此时有 8分
8分
∴ 9分
9分
②又设 ,先求
,先求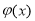 与
与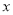 轴在
轴在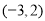 的交点
的交点
∵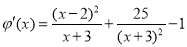 ,由
,由 得
得
故 ,
,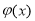 在
在 单调递增
单调递增
又 ,故
,故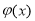 与
与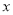 轴有唯一交点
轴有唯一交点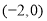
即 与
与 的图象在区间
的图象在区间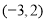 上的唯一交点坐标为
上的唯一交点坐标为 为所求 13分.
为所求 13分.
考点:1.分类讨论的思想;2.函数的导数与单调性;3.二次函数的图像与性质;4.两函数图像的交点问题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源:2015届河北唐山一中高二下学期期末考试理科数学试卷(解析版) 题型:选择题
命题“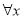 ∈R,
∈R,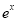 -x+1≥0”的否定是( )
-x+1≥0”的否定是( )
A.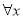 ∈R,lnx+x+1<0 B.
∈R,lnx+x+1<0 B.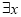 ∈R,
∈R,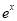 -x+1<0
-x+1<0
C.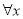 ∈R,
∈R,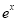 -x+1>0 D.
-x+1>0 D.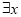 ∈R,
∈R,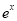 -x+1≥0
-x+1≥0
查看答案和解析>>
科目:高中数学 来源:2015届河北保定高阳中学、定兴三中高二下学期期末文数学卷(解析版) 题型:选择题
已知幂函数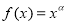 的部分对应值如下表:
的部分对应值如下表:
x | 1 |
|
f(x) | 1 |
|
则不等式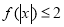 的解集是( ).
的解集是( ).
A.{x|-4≤x≤4} B.{x|0≤x≤4}
C.{x|- ≤x≤
≤x≤ } D.{x|0<x≤
} D.{x|0<x≤ }
}
查看答案和解析>>
科目:高中数学 来源:2015届河北保定高阳中学、定兴三中高二下学期期末文数学卷(解析版) 题型:选择题
若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“同族函数”,则函数解析式为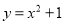 ,值域为{1,3}的同族函数有( ).
,值域为{1,3}的同族函数有( ).
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源:2015届江西省高二下学期期中考试文科数学试卷(解析版) 题型:填空题
科研人员研究某物质的溶解度 与温度
与温度 之间的关系,得到如下表部分数据,则其回归直线方程为 (
之间的关系,得到如下表部分数据,则其回归直线方程为 ( ,其中
,其中 ).
).
温度 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
溶解度 | 90 | 84 | 83 | 80 | 75 | 68 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com