(1)若不等式x2+4x+6-a≥0当-3≤x≤1时有解,求实数a的取值范围;
(2)对任意a∈[-1,1],函数f(x)=x2+(a-4)x+4-2a的值恒大于零,求实数x的取值范围.
【答案】
分析:(1)原不等式等价于x
2+4x+6≥a,因此问题转化为函数y=x
2+4x+6在[-3,1]上的最大值大于或等于a,结合二次函数的单调性算出当x=1时,y=x
2+4x+6的最大值等于11,即可求出实数a的取值范围;
(2)函数化简为f(x)=g(a)=a(x-2)+x
2-4x+4,是关于a的一次函数.因此根据一次函数的单调性,结合题意建立关于x的不等式组,解之即可得到实数x的取值范围.
解答:解:(1)不等式x
2+4x+6-a≥0,即x
2+4x+6≥a
因此,原不等式当-3≤x≤1时有解,
即y=x
2+4x+6在[-3,1]上的最大值大于或等于a
∵y=x
2+4x+6=(x+2)
2+2,
在[-3,-2]上是减函数;在[-2,1]上是增函数;
∴当x=1时,y=x
2+4x+6的最大值等于11
所以不等式x
2+4x+6-a≥0当-3≤x≤1时有解时a≤11,即实数a的取值范围为(-∞,11];
(2)∵f(x)=x
2+(a-4)x+4-2a=a(x-2)+x
2-4x+4,
可得f(x)=g(a)=a(x-2)+x
2-4x+4,是关于a的一次函数
∴对任意a∈[-1,1],函数f(x)=x
2+(a-4)x+4-2a的值恒大于零,
即g(-1)>0且g(1)>0,可得
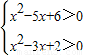
,解之得x<1或>3
即满足条件的实数x的取值范围为(-∞,1]∪[3,+∞).
点评:本题给出含有字母参数的函数,求不等式恒成立时参数的取值范围.着重考查了二次函数、一次函数的图象与性质和不等式恒成立的理解等知识,属于中档题.

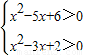 ,解之得x<1或>3
,解之得x<1或>3
