
如图,在四棱锥 中,
中, 底面
底面 ,底面
,底面 是平行四边形,
是平行四边形, ,
, 是
是 的中点。
的中点。

(1)求证: ;
;
(2)求证: ;
;
(3)若 ,求二面角
,求二面角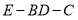 的余弦值.
的余弦值.
(1)详见解析;(2)详见解析;(3)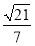
【解析】
试题分析:(1)连接AC交BD于F,连接EF,由ABCD是平行四边形,知F为AC的中点,由E为SC的中点,知SA∥EF,由此能够证明SA∥平面BDE.
(2)由AB=2,AD=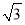 ,∠BAD=30°,利用余弦定理得BD=1,由AD2+BD2=AB2,知AD⊥BD.由此能够证明AD⊥SB.
,∠BAD=30°,利用余弦定理得BD=1,由AD2+BD2=AB2,知AD⊥BD.由此能够证明AD⊥SB.
(3)以DA为x轴,以DB为y轴,以DS为z轴,建立空间直角坐标系,利用向量法能够求出二面角E-BD-C的余弦值.
试题解析:(1)证明:连接AC交BD于F,连结EF,由ABCD是平行四边形,知F为AC的中点,又E为SC的中点,所以SA∥EF,∵SA?平面BDE,EF?平面BDE,
∴SA∥平面BDE. 4分
(2)由AB=2,AD=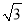 ,∠BAD=30?,由余弦定理得
,∠BAD=30?,由余弦定理得
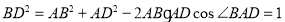
∵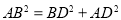 ∴AD⊥BD.
∴AD⊥BD.
∵SD⊥平面ABCD,AD?平面ABCD,
∴AD⊥SD,
∴AD⊥平面SBD,又SB?平面SBD,
∴AD⊥SB. 8分
(3)取CD的中点G,连结EG,FG,

则EG⊥平面BCD,且EG=1,FG∥BC,且FG=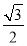
∵AD⊥BD, AD∥BC,∴FG⊥BD,又∵EG⊥BD ∴BD⊥平面EFG,
∴BD⊥EF,故∠EFG是二面角E—BD—C的平面角
在Rt△EFG中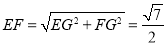
∴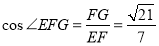 . 12分
. 12分
考点:(1)空间线面的位置关系;(2)二面角的求法;(3)向量在立体几何中的应用.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源:2015届北京东城(南片)高二上学期期末考试理数学试卷(解析版) 题型:选择题
一组数据的方差是s2,将这组数据中的每一个数据都乘以2,所得到的一组数据的方差是
A. 2s2 B. 4s2 C. 8s2 D. 16s2
查看答案和解析>>
科目:高中数学 来源:2015届云南玉溪一中高二上学期期末考试理科数学试卷(解析版) 题型:填空题
下列说法:
① “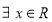 ,使
,使 >3”的否定是“
>3”的否定是“ ,使
,使 3”;
3”;
② 函数 的最小正周期是
的最小正周期是 ;
;
③ “在 中,若
中,若 ,则
,则 ”的逆命题是真命题;
”的逆命题是真命题;
④ “ ”是“直线
”是“直线 和直线
和直线 垂直”的充要条件;其中正确的说法是 (只填序号).
垂直”的充要条件;其中正确的说法是 (只填序号).
查看答案和解析>>
科目:高中数学 来源:2015届云南玉溪一中高二上学期期末考试文科数学试卷(解析版) 题型:选择题
椭圆 ,
,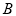 为上顶点,
为上顶点, 为左焦点,
为左焦点,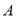 为右顶点,且右顶点
为右顶点,且右顶点 到直线
到直线 的距离为
的距离为 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )
A. B.
B. C.
C. D.
D. 
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习真题感悟常考问题7练习卷(解析版) 题型:选择题
在△ABC中,∠ABC= ,AB=
,AB= ,BC=3,则sin ∠BAC=( ).
,BC=3,则sin ∠BAC=( ).
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com