
【题目】数学名著《算学启蒙》中有关于“松竹并生”的问题:松长四尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图,是源于其思想的一个程序框图.若输入的![]() 分别为8、2,则输出的
分别为8、2,则输出的![]() ( )
( )
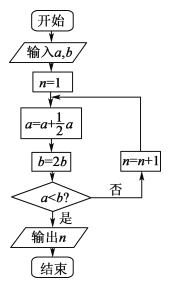
A. 2 B. 3 C. 4 D. 5
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
【题目】中国共产党第十九次全国代表大会于2017年10月18日至10月24日在北京召开,会议提出“决胜全面建成小康社会”.某市积极响应开展“脱贫攻坚”,为2020年“全面建成小康社会”贡献力量.为了解该市农村“脱贫攻坚”情况,从某县调查得到农村居民2013年至2017年家庭人均纯收入![]() (单位:百元)的数据如表:
(单位:百元)的数据如表:
年 份 | 2013 | 2014 | 2015 | 2016 | 2017 |
年人均纯收入 | 47 | 55 | 61 | 65 | 72 |
注:小康的标准是农村居民家庭年人均纯收入达到8000元.
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,预测2020年该县农村居民家庭年人均纯收入指标能否达到“全面建成小康社会”的标准?
附:回归直线![]() 斜率和截距的最小二乘估计公式分别为:
斜率和截距的最小二乘估计公式分别为:
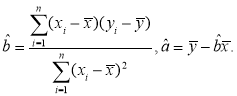
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线![]() 的焦点
的焦点![]() ,斜率为
,斜率为![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,且
两点,且![]() .
.
(1)求该抛物线![]() 的方程;
的方程;
(2)已知抛物线上一点![]() ,过点
,过点![]() 作抛物线的两条弦
作抛物线的两条弦![]() 和
和![]() ,且
,且![]() ,判断直线
,判断直线![]() 是否过定点?并说明理由.
是否过定点?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图给出的是2000年至2016年我国实际利用外资情况,以下结论正确的是( )
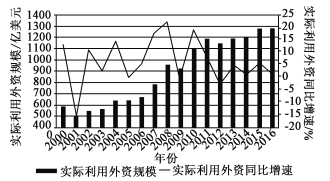
A. 2000年以来我国实际利用外资规模与年份呈负相关
B. 2010年以来我国实际利用外资规模逐年增大
C. 2008年以来我国实际利用外资同比增速最大
D. 2010年以来我国实际利用外资同比增速最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学回答“用数学归纳法的证明![]() (n∈N*)”的过程如下:
(n∈N*)”的过程如下:
证明:①当n=1时,显然命题是正确的.②假设当n=k(k≥1,k∈N*)时,有![]() ,那么当n=k+1时,
,那么当n=k+1时,![]() ,所以当n=k+1时命题是正确的,由①②可知对于n∈N*,命题都是正确的,以上证法是错误的,错误在于( )
,所以当n=k+1时命题是正确的,由①②可知对于n∈N*,命题都是正确的,以上证法是错误的,错误在于( )
A.从k到k+1的推理过程没有使用归纳假设
B.假设的写法不正确
C.从k到k+1的推理不严密
D.当n=1时,验证过程不具体
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的顶点在原点,过点A(-4,4)且焦点在x轴.
(1)求抛物线方程;
(2)直线l过定点B(-1,0)与该抛物线相交所得弦长为8,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了支援湖北省应对新冠肺炎,某运输公司现有5名男司机,4名女司机,需选派5人运输一批紧急医用物资到武汉.
(1)如果派3名男司机、2名女司机,共有多少种不同的选派方法?
(2)至少有两名男司机,共有多少种不同的选派方法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上, ![]() 是等边三角形.
是等边三角形.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)点![]() 在椭圆
在椭圆![]() 上,线段
上,线段![]() 与线段
与线段![]() 交于点
交于点![]() ,若
,若![]() 与
与![]() 的面积之比为
的面积之比为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com