练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某租赁公司拥有汽车100辆，当每辆车的月租金为3 000元时，可全部租出；当每辆车的月租金增加50元时，未租出的车将会增加一辆．租出的车辆每月需要维护费200元．

    (1)当每辆车月租金为3 600元时，能租出多少辆车？

    (2)当每辆车的月租金为多少元时，租赁公司的月收益最大？最大月收益是多少元？


    解：(1)当每辆车的月租金定为3 600元时，未租出的车辆数为＝12，所以这时租出了88辆车．

    (2)设每辆车的月租金定为x(x≥3 000)元，则租赁公司的月收益为

    f(x)＝ (x－200)，整理得

    f(x)＝(8 000－x)(x－200)＝－x2＋164x－32 000

    ＝－(x－4 100)2＋304 200.

    所以，当x＝4 100时，f(x)最大．

    最大值为f(4 100)＝304 200，即当每辆车的月租金定为4 100元时，租赁公司的月收益最大，最大月收益为304 200元．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    一质点在直线上从时刻t＝0(s)开始以速度v＝t2－4t＋3(m/s)运动．求：

    (1)在t＝4 s的位置；(2)在t＝4 s内运动的路程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    定义在R上的函数f(x)满足f(x)＋f(x＋5)＝16，当x∈(－1,4]时， f(x)＝x2－2x，则函数f(x)在[0,2 013]上的零点个数是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)的图象与函数h(x)＝x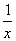＋＋2的图象关于点A(0,1)对称．

    (1)求函数f(x)的解析式；

    (2)若g(x)＝f(x)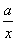＋，g(x)在区间(0,2]上的值不小于6，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示的四个容器高度都相同，将水从容器顶部一个小孔以相同的速度注入其中，注满为止．用下面对应的图象显示该容器中水面的高度h和时间t之间的关系，其中不正确的是(　　)

    A．1个  B．2个  C．3个  D．4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若平面向量a，b满足|a＋b|＝1，且a＝2b，则|b|＝(　　)

    A.  B.  C．1  D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设点M是线段BC的中点，点A在直线BC外＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a＝(1,2)，b＝(－2，n)，a与b的夹角是45°.

    (1)求b；

    (2)若c与b同向，且a与c－a垂直，求c.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝x2在x0到x0＋Δx之间的平均变化率为k1，在x0－Δx到x0之间的平均变化率为k2，则k1，k2的大小关系是(　　)

    A．k1＜k2                                             B．k1＞k2

    C．k1＝k2                                             D．无法确定

    查看答案和解析>>

    同步练习册答案