
| an | an+2 |
| an |
| an+2 |
| 1 |
| an |
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
| 1 |
| an+1 |
| an+2 |
| an |
| 2 |
| an |
| 1 |
| an+1 |
| 1 |
| an |
| ||
|
| 1 |
| a1 |
| 1 |
| an |
| 1 |
| an |
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
| 2n |
| (2n-1)(2n+1-1) |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
| 1 |
| 21-1 |
| 1 |
| 22-1 |
| 1 |
| 22-1 |
| 1 |
| 23-1 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
| 1 |
| 2n+1-1 |
| an |
| an+2 |


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| n |
| n |
| 2 |
| 4an-5 |
查看答案和解析>>
科目:高中数学 来源:2004年高考教材全程总复习试卷·数学 题型:013
已知{an}满足,对一切自然数n均有an+1>an,且an=n2+λn恒成立,则实数λ的取值范围是
[ ]
查看答案和解析>>
科目:高中数学 来源:江西省六校2010届高三下学期联考数学文科试题 题型:044
已知定义域为R的二次函数f(x)的最小值为0,且有f(1+x)=f(1-x),直线g(x)=4(x-1)的图象被f(x)的图象截得的弦长为4![]() ,数列{an}满足a1=2,
,数列{an}满足a1=2,
(an+1-an)g(an)+f(an)=0(n∈N*).
(1)求函数f(x)的解析式;
(2)求数列{an}的通项公式;
(3)设bn=3f(an)-g(an+1),求数列{bn}的最值及相应的n值.
查看答案和解析>>
科目:高中数学 来源:湖南省高考真题 题型:解答题
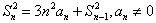 ,n=2,3,4,…
,n=2,3,4,… 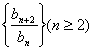 是常数数列;
是常数数列;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com