
下面四个命题,正确的是( )
A.己知直线a,b?平面α,直线c?平面β,若c⊥a,c⊥b,则平面α⊥平面β
B.若直线a平行平面α内的无数条直线,则直线a∥平面α
C.若直线a垂直直线b在平面a内的射影,则直线a⊥b
D.若直线a,b.c两两成异面直线,则一定存在直线与a,b,c都相交
D
【解析】
试题分析:在A中,只有当a,b相交时,才有平面α⊥平面β;在B中,当直线a平行平面α内的无数条平行直线时,则直线a不一定平行于平面α;在C中,直线a垂直直线b在平面a内的射影,则直线a,b相交或垂直;在D中,若直线a,b.c两两成异面直线,则一定存在直线与a,b,c都相交.
【解析】
在A中,只有当a,b相交时,才有平面α⊥平面β,故A不正确;
在B中,当直线a平行平面α内的无数条平行直线时,
则直线a不一定平行于平面α,故B不正确;
在C中,直线a垂直直线b在平面a内的射影,则直线a,b相交或垂直;
在D中,若直线a,b.c两两成异面直线,
则一定存在直线与a,b,c都相交,故D成立.
故选D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:[同步]2015年人教B版必修二2.1平面直角坐标系中的基本公式练习卷(解析版) 题型:解答题
求证:若圆内接四边形的两条对角线互相垂直,则从对角线交点到一边中点的线段长等于圆心到该边对边的距离.
查看答案和解析>>
科目:高中数学 来源:[同步]2015年人教A版必修二4.3 空间直角坐标系练习卷(解析版) 题型:
已知点A(1,2,1),B(﹣1,3,4),D(1,1,1),若 =2
=2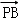 ,则|
,则| |的值是 .
|的值是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2015人教B版选修4-5 3.2用数学归纳法证明不等式练习卷(解析版) 题型:填空题
用数学归纳法证明 +cosα+cos3α+…+cos(2n﹣1)α=
+cosα+cos3α+…+cos(2n﹣1)α=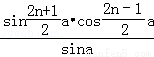 (k∈Z*,α≠kπ,n∈N+),在验证n=1时,左边计算所得的项是 .
(k∈Z*,α≠kπ,n∈N+),在验证n=1时,左边计算所得的项是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2015人教A版必修二2.1空间点、直线、平面间位置关系练习卷(解析版) 题型:
用符号表示“点A在直线上l,直线l在平面α外”,正确的是( )
A.A∈l,l∉α B.A∈l,l?α C.A?l,l?α D.A?l,l∉α
查看答案和解析>>
科目:高中数学 来源:[同步]2015人教A版必修二2.1空间点、直线、平面间位置关系练习卷(解析版) 题型:
在三棱柱ABC﹣A1B1C1中,各棱长相等,侧棱垂直于底面,点D是侧面BB1C1C的中心,则AD与平面BB1C1C所成角的大小是( )
A.30° B.45° C.60° D.90°
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-2 4.1变换的不变量 矩阵特征向量(解析版) 题型:填空题
选修4﹣2:矩阵与变换已知二阶矩阵M有特征值λ=3及对应的一个特征向量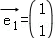 ,并且矩阵M对应的变换将点(﹣1,2)变换成(3,0),求矩阵M.
,并且矩阵M对应的变换将点(﹣1,2)变换成(3,0),求矩阵M.
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习(解析版) 题型:填空题
(2014•咸阳一模)(选修4﹣1 几何证明选讲)如图,两个等圆⊙O与⊙O′外切,过O作⊙O′的两条切线OA,OB,A,B是切点,点C在圆O′上且不与点A,B重合,则∠ACB= .
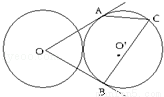
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理(解析版) 题型:选择题
如图所示,圆的内接△ABC的∠C的平分线CD延长后交圆于点E,连接BE,已知BD=3,CE=7,BC=5,则线段BE=( )
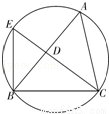
A. B.
B.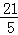 C.
C.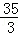 D.4
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com