
����С������12�֣�
ijѧУ�߶��꼶����1000��ѧ������������650�ˣ�Ů��350�ˣ�Ϊ�˵���ѧ����ĩ�����з�ʽ���÷ֲ�����ķ��������200��ѧ��.
��1���������� ��������
��������
|
|
��ϲ���˶� |
ϲ���˶� |
�ϼ� |
|
�� |
50 |
|
|
|
���� |
|
|
|
|
�ϼ� |
|
100 |
200 |
��2����ϲ���˶���Ů���е������ǵ��˶�ʱ�䣬 �������ǵ��˶�ʱ�����30���ӵ�90����֮�䣬��ͼ�Dz��������Ƶ�ʷֲ�ֱ��ͼ�����������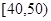 ��
��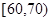 ������Ů���������ȡ����Ů���������ǵ��˶�ʱ����ͬһ����εĸ���.
������Ů���������ȡ����Ů���������ǵ��˶�ʱ����ͬһ����εĸ���.
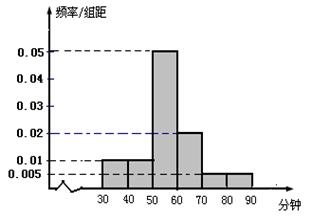
��1�������������������2��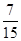 .
.
��������
�����������1�����÷ֲ�����������2������Ƶ�ʷֲ�ֱ��ͼ��� �ڵ���������
�ڵ���������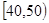 ���������г����е�������г�����.
����������������������.
�����������1�����ݷֲ�����Ķ��壬֪��ȡ����130�ˣ�Ů��70�ˣ� 1��
|
|
��ϲ���˶� |
ϲ���˶� |
�ϼ� |
|
�� |
50 |
20 |
70 |
|
���� |
50 |
80 |
130 |
|
�ϼ� |
100 |
100 |
200 |
3��
��2����ֱ��ͼ֪�� �ڵ�����Ϊ4�ˣ���Ϊ
�ڵ�����Ϊ4�ˣ���Ϊ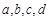 .
.
��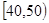 ������Ϊ2�ˣ���Ϊ
������Ϊ2�ˣ���Ϊ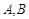 .
5��
.
5��
����6������ѡ2����AB,Aa,Ab,Ac,Ad,Ba,Bb,Bc,Bd,ab,ac,ad,bc,bd,cd
��15����� 7��
�� ʱ����
ʱ����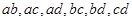 ����������� 9��
����������� 9��
�� ʱ����
ʱ����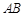 һ�������
10��
һ�������
10��
�¼�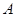 :��������ͬһ����Ρ��������Ļ����¼�������
:��������ͬһ����Ρ��������Ļ����¼�������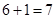 �֣� 11��
�֣� 11��
�� 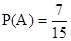
������Ů�����˶�ʱ����ͬһ����εĸ���Ϊ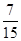 .
12��
.
12��
���㣺1.�ֲ������2.Ƶ�ʷֲ�ֱ��ͼ.


 ��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д� ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| ON |
| ON |
| 5 |
| OM |
| OT |
| M1M |
| N1N |
| OP |
| OA |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����С������12�֣���֪����![]() ����
����![]() ������
������![]() �����ֵ����Сֵ������
�����ֵ����Сֵ������![]() ���ڶ������ϵĵ�������.
���ڶ������ϵĵ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��2009���Ͼ��ģ�����С������12�֣�
Ϊ��������������ij�о����½�һ���ص㹤�̣��ֱ�Ϊ������ʩ���̡��������̺Ͳ�ҵ���蹤�����࣬�������������Ŀ�ĸ����ֱ�ռ������![]() ��
��![]() ��
��![]() .����3�����˶����ش�����ѡһ����Ŀ���뽨��.��
.����3�����˶����ش�����ѡһ����Ŀ���뽨��.��
��I������ѡ�����Ŀ���������ͬ�ĸ��ʣ� w.w.w.k.s.5.u.c.o.m ![]()
![]()
��II��������1��ѡ�����Ŀ�����������̵ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����С������12�֣�
ij��Ӫ��ҵ����A��B���ֲ�Ʒ�������г������Ԥ�⣬A��Ʒ��������Ͷ�ʳ����ȣ����ϵ��ͼ1��B��Ʒ��������Ͷ�ʵ�����ƽ���������ȣ����ϵ��ͼ2��
��ע��������Ͷ�ʵ�λ����Ԫ��
��1���ֱ�A��B���ֲ�Ʒ�������ʾΪͶ�ʵĺ�������д�����ǵĺ�����ϵʽ.��2������ҵ�ѳO��10��Ԫ�ʽ𣬲�ȫ��Ͷ�뵽A��B���ֲ�Ʒ���������ʣ�����������10��ԪͶ�ʣ�����ʹ��ҵ�������������������Ϊ������Ԫ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com