
 圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知点P(x0,y0)、M(m,n)是圆锥曲线C上不与顶点重合的任意两点,MN是垂直于x轴的一条垂轴弦,直线MP、NP分别交x轴于点E(xE,0)和点F(xF,0).
圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知点P(x0,y0)、M(m,n)是圆锥曲线C上不与顶点重合的任意两点,MN是垂直于x轴的一条垂轴弦,直线MP、NP分别交x轴于点E(xE,0)和点F(xF,0).| x2 |
| a2 |
| y2 |
| b2 |
| m2y02-n2x02 |
| y02-n2 |
| x2 |
| a2 |
| y2 |
| b2 |
| y0-n |
| x0-m |
| my0-nx0 |
| y0-n |
| my0+nx0 |
| y0+n |
| m2y02-n2x02 |
| y02-n2 |
| x2 |
| a2 |
| y2 |
| b2 |
| m2 |
| a2 |
| x02 |
| a2 |
m2b2(1-
| ||||
b2(1-
|
| b2(m2-x02) | ||
|
| m2y02-n2x02 |
| y02-n2 |
| m2(R2-x02)-(R2-m2)x02 |
| (R2-x02)-(R2-m2) |
| R2(m2-x02) |
| (m2-x02) |
| x2 |
| a2 |
| y2 |
| b2 |
| m2y02-n2x02 |
| y02-n2 |
| x2 |
| a2 |
| y2 |
| b2 |
| m2 |
| a2 |
| x02 |
| a2 |
m2b2(
| ||||
b2(
|
| b2(x02-m2) | ||
|
| 2(my02-n2x0) |
| y02-n2 |
| 2(my02-n2x0) |
| y02-n2 |
| 2(m2px0-2pmx0) |
| y02-n2 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知椭圆C:
圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知椭圆C:| x2 |
| 4 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知点P(
圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知点P(| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年上海市徐汇区高三上学期期末理科数学卷 题型:解答题
圆锥曲线上任意两点连成的线段称为弦。若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦。已知点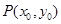 、
、 是圆锥曲线C
是圆锥曲线C 上不与顶点重合的任意两点,
上不与顶点重合的任意两点, 是垂直于
是垂直于 轴的一条垂轴弦,直线
轴的一条垂轴弦,直线 分别交
分别交 轴于点
轴于点 和点
和点 。
。

(1)试用 的代数式分别表示
的代数式分别表示 和
和 ;
;
(2)若C的方程为 (如图),求证:
(如图),求证: 是与
是与 和点
和点 位置无关的定值;
位置无关的定值;
(3)请选定一条除椭圆外的圆锥曲线C,试探究 和
和 经过某种四则运算(加、减、乘、除),其
经过某种四则运算(加、减、乘、除),其 结果是否是与
结果是否是与 和点
和点 位置无关的定值,写出你的研究结论并证明。
位置无关的定值,写出你的研究结论并证明。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省镇江市扬中二中高三(上)期末数学模拟试卷(解析版) 题型:解答题
 ”.类比这一结论,我们猜想:“若曲线C的方程为
”.类比这一结论,我们猜想:“若曲线C的方程为 (如图),则xE•xF也是与点M、N、P位置无关的定值”,请你对该猜想给出证明.
(如图),则xE•xF也是与点M、N、P位置无关的定值”,请你对该猜想给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com