
 Բ�����������������ɵ��߶γ�Ϊ�ң���Բ�����ϵ�һ���Ҵ�ֱ����Գ��ᣬ���ǽ����ҳ�֮Ϊ���ߵĴ����ң���֪��P��
Բ�����������������ɵ��߶γ�Ϊ�ң���Բ�����ϵ�һ���Ҵ�ֱ����Գ��ᣬ���ǽ����ҳ�֮Ϊ���ߵĴ����ң���֪��P��| x2 |
| a2 |
| y2 |
| b2 |
| y0-m |
| x0-m |
| my0-nx0 |
| y0-n |
| my0+nx0 |
| y0+n |
| my0-nx0 |
| y0-n |
| my0+nx0 |
| y0+n |
| ||||
|
| x2 |
| a2 |
| y2 |
| b2 |
| m2 |
| a2 |
| y | 2 0 |
| x02 |
| a2 |
| ||||
|
| ||||
|



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 Բ�����������������ɵ��߶γ�Ϊ�ң���Բ�����ϵ�һ���Ҵ�ֱ����Գ��ᣬ���ǽ����ҳ�֮Ϊ���ߵĴ����ң���֪��P��x0��y0����M��m��n����Բ����C�ϲ��붥���غϵ��������㣬MN�Ǵ�ֱ��x���һ�������ң�ֱ��MP��NP�ֱ�x���ڵ�E��xE��0���͵�F��xF��0����
Բ�����������������ɵ��߶γ�Ϊ�ң���Բ�����ϵ�һ���Ҵ�ֱ����Գ��ᣬ���ǽ����ҳ�֮Ϊ���ߵĴ����ң���֪��P��x0��y0����M��m��n����Բ����C�ϲ��붥���غϵ��������㣬MN�Ǵ�ֱ��x���һ�������ң�ֱ��MP��NP�ֱ�x���ڵ�E��xE��0���͵�F��xF��0����| x2 |
| a2 |
| y2 |
| b2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 Բ�����������������ɵ��߶γ�Ϊ�ң���Բ�����ϵ�һ���Ҵ�ֱ����Գ��ᣬ���ǽ����ҳ�֮Ϊ���ߵĴ����ң���֪��ԲC��
Բ�����������������ɵ��߶γ�Ϊ�ң���Բ�����ϵ�һ���Ҵ�ֱ����Գ��ᣬ���ǽ����ҳ�֮Ϊ���ߵĴ����ң���֪��ԲC��| x2 |
| 4 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010-2011ѧ���Ϻ��������������ѧ����ĩ������ѧ�� ���ͣ������
Բ�����������������ɵ��߶γ�Ϊ�ҡ���Բ�����ϵ�һ���Ҵ�ֱ����Գ��ᣬ���ǽ����ҳ�֮Ϊ���ߵĴ����ҡ���֪��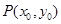 ��
�� ��Բ����C
��Բ����C �ϲ��붥���غϵ��������㣬
�ϲ��붥���غϵ��������㣬 �Ǵ�ֱ��
�Ǵ�ֱ�� ���һ�������ң�ֱ��
���һ�������ң�ֱ�� �ֱ�
�ֱ� ���ڵ�
���ڵ� �͵�
�͵� ��
��

��1������ �Ĵ���ʽ�ֱ��ʾ
�Ĵ���ʽ�ֱ��ʾ ��
�� ��
��
��2����C�ķ���Ϊ ����ͼ������֤��
����ͼ������֤�� ����
���� �͵�
�͵� λ���صĶ�ֵ��
λ���صĶ�ֵ��
��3����ѡ��һ������Բ���Բ����C����̽�� ��
�� ����ij���������㣨�ӡ������ˡ���������
����ij���������㣨�ӡ������ˡ��������� ����Ƿ�����
����Ƿ����� �͵�
�͵� λ���صĶ�ֵ��д������о����۲�֤����
λ���صĶ�ֵ��д������о����۲�֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012-2013ѧ�꽭��ʡ�������ж��и������ϣ���ĩ��ѧģ���Ծ��������棩 ���ͣ������
 ���������һ���ۣ����Dz��룺��������C�ķ���Ϊ
���������һ���ۣ����Dz��룺��������C�ķ���Ϊ ����ͼ������xE•xFҲ�����M��N��Pλ���صĶ�ֵ��������Ըò������֤����
����ͼ������xE•xFҲ�����M��N��Pλ���صĶ�ֵ��������Ըò������֤����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com