[题目]钝角三角形ABC的面积是 .AB=1.BC= .则AC=( )A.5B.C.2D.1 题目和参考答案——青夏教育精英家教网—

【题目】钝角三角形ABC的面积是，AB=1，BC= ，则AC=（）
A.5
B.
C.2
D.1

【答案】B
【解析】解：∵钝角三角形ABC的面积是，AB=c=1，BC=a= ，
∴S= acsinB= ，即sinB= ，
当B为钝角时，cosB=﹣ =﹣ ，
利用余弦定理得：AC2=AB2+BC2﹣2ABBCcosB=1+2+2=5，即AC= ，
当B为锐角时，cosB= = ，
利用余弦定理得：AC2=AB2+BC2﹣2ABBCcosB=1+2﹣2=1，即AC=1，
此时AB2+AC2=BC2 ，即△ABC为直角三角形，不合题意，舍去，
则AC= ．
故选：B．
【考点精析】解答此题的关键在于理解余弦定理的定义的相关知识，掌握余弦定理:;;．

练习册系列答案

南大励学小学生英语四合一阅读组合训练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，在直角△ABC中，AB⊥BC，D为BC边上异于B、C的一点，以AB为直径作⊙O，并分别交AC，AD于点E，F．

（1）证明：C，E，F，D四点共圆；
（2）若D为BC的中点，且AF=3，FD=1，求AE的长．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】函数的性质通常指函数的定义域、值域、周期性、单调性、奇偶性、对称性等，请选择适当的探究顺序，研究函数的性质，并在此基础上填写下表，作出f（x）在区间[-π，2π]上的图象．

性质	理由	结论	得分
定义域
值域
奇偶性
周期性
单调性
对称性
作图

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图在长为10千米的河流的一侧有一条观光带，观光带的前一部分为曲线段，设曲线段为函数（单位：千米）的图象，且图象的最高点为；观光带的后一部分为线段．

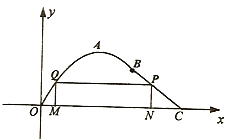
（1）求函数为曲线段的函数的解析式；

（2）若计划在河流和观光带之间新建一个如图所示的矩形绿化带，绿化带仅由线段构成，其中点在线段上．当长为多少时，绿化带的总长度最长？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=x2（lnx+lna）（a＞0）．
（1）当a=1时，设函数g（x）= ，求函数g（x）的单调区间与极值；
（2）设f′（x）是f（x）的导函数，若 ≤1对任意的x＞0恒成立，求实数a的取值范围；
（3）若x1 ， x2∈（，1），x1+x2＜1，求证：x1x2＜（x1+x2）4 ．