
【题目】函数的性质通常指函数的定义域、值域、周期性、单调性、奇偶性、对称性等,请选择适当的探究顺序,研究函数![]() 的性质,并在此基础上填写下表,作出f(x)在区间[-π,2π]上的图象.
的性质,并在此基础上填写下表,作出f(x)在区间[-π,2π]上的图象.
性质 | 理由 | 结论 | 得分 |
定义域 | |||
值域 | |||
奇偶性 | |||
周期性 | |||
单调性 | |||
对称性 | |||
作图 |
| ||
【答案】详见解析
【解析】
由正弦函数的最大最小值,可得函数的定义域为R;由平方法结合余弦函数的有界性,得到函数的值域为[![]() ,2];由函数周期性的定义加以验证,得到函数的最小正周期为π;讨论函数在区间[0,π]上的单调性,结合函数的周期可得函数在R上的单调区间;最后根据函数奇偶性的定义和轴对称的有关公式,算出f(x)在其定义域上为偶函数,图象关于直线
,2];由函数周期性的定义加以验证,得到函数的最小正周期为π;讨论函数在区间[0,π]上的单调性,结合函数的周期可得函数在R上的单调区间;最后根据函数奇偶性的定义和轴对称的有关公式,算出f(x)在其定义域上为偶函数,图象关于直线![]() 对称.由此即可得到本题的答案.
对称.由此即可得到本题的答案.
∵1-sinx≥0且1+sinx≥0,在R上恒成立
∴函数的定义域为R;
∵![]() =2+2|cosx|
=2+2|cosx|
∴由|cosx|∈[0,1],f2(x)∈[2,4],可得函数的值域为[![]() ,2];
,2];
∵![]() =f(x)
=f(x)
∴函数的最小正周期为π
∵当x∈[0,![]() ]时,
]时,![]() =2cos
=2cos![]() ,在[0,
,在[0,![]() ]上为减函数
]上为减函数
当x∈[![]() ,π]时,
,π]时,![]() =2sin
=2sin![]() ,在[
,在[![]() ,π]上为增函数
,π]上为增函数
∴f(x)在![]() 上递增,在
上递增,在![]() 上递减(k∈Z)
上递减(k∈Z)
∵f(-x)=f(x)且![]() ,
,
∴f(x)在其定义域上为偶函数,结合周期为π得到图象关于直线![]() 对称
对称
因此,可得如下表格:
性质 | 理由 | 结论 | 得分 |
定义域 | -1≤sinx≤1 | 定义域R | |
值域 | y2=2+2|cosx|∈[2,4] | 值域 | |
奇偶性 | f(-x)=f(x) | 偶函数 | |
周期性 | f(x+π)=f(x) | 周期T=π | |
单调性 |
| 在 在 | |
对称性 | f(-x)=f(x), | 关于直线 | |
作图 |
| ||


科目:高中数学 来源: 题型:
【题目】如图所示,正方体![]() 的棱长为1,线段
的棱长为1,线段![]() 上有两个动点
上有两个动点![]() ,且
,且![]() ,则下列结论中正确的是__________.
,则下列结论中正确的是__________.
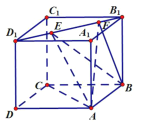
①![]() 平面
平面![]() ;
;
②平面![]() 平面
平面![]() ;
;
③三棱锥![]() 的体积为定值;
的体积为定值;
④存在某个位置使得异面直线![]() 与
与![]() 成角
成角![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 满足:①圆心在第一象限,截
满足:①圆心在第一象限,截![]() 轴所得弦长为2;②被
轴所得弦长为2;②被![]() 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为![]() ;③圆心到直线
;③圆心到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)若点![]() 是直线
是直线![]() 上的动点,过点
上的动点,过点![]() 分别做圆
分别做圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
, ![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C经过点(3,6)且焦点在x轴上.
(1)求抛物线C的标准方程;
(2)直线l: ![]() 过抛物线C的焦点F且与抛物线C交于A,B两点,求A,B两点间的距离.
过抛物线C的焦点F且与抛物线C交于A,B两点,求A,B两点间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x),g(x)满足关系g(x)=f(x)f(x+α),其中α是常数.
(1)设f(x)=cosx+sinx,![]() ,求g(x)的解析式;
,求g(x)的解析式;
(2)设计一个函数f(x)及一个α的值,使得![]() ;
;
(3)当f(x)=|sinx|+cosx,![]() 时,存在x1,x2∈R,对任意x∈R,g(x1)≤g(x)≤g(x2)恒成立,求|x1-x2|的最小值.
时,存在x1,x2∈R,对任意x∈R,g(x1)≤g(x)≤g(x2)恒成立,求|x1-x2|的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com