Question

【题目】已知椭圆 抛物线 焦点均在 轴上， 的中心和 顶点均为原点 ，从每条曲线上各取两个点，将其坐标记录于表中，则 的左焦点到 的准线之间的距离为（ ）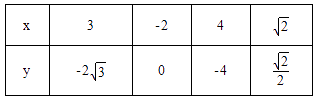

A.
B.
C.1
D.2

Answer 1

【答案】B
【解析】解：A、∵由表可知，抛物线 焦点在 轴的正半轴，设抛物线 ,则有 , ∴将 代入 ，代入可得 ,即 ∴抛物线 的标准方程为 ，则焦点坐标为 ,准线方程为 , 设椭圆 ,把点 代入得, ，即 ∴ 的标准方程为 ; ∵ ∴左焦点 ∴ 的左焦点到 C2 的准线之间的距离 1,A不符合题意

B、 C1 的左焦点到 C2 的准线之间的距离 1，B符合题意；
C、 C1 的左焦点到 C2 的准线之间的距离 1，C不符合题意；
D、 C1 的左焦点到 C2 的准线之间的距离 1，D不符合题意。
故答案为：B.

过定点的椭圆方程可以设为：mX2+nY2=1;焦点在X轴上的椭圆方程可以设为：+=1（a>b>0）；有共同焦点（，0）的椭圆方程可以设为：=1等。焦点在X轴的正半轴上的抛物线的标准方程可以设为：Y2=2px（p>0）；焦点在X轴的负半轴上的抛物线的标准方程可以设为：Y2=-2px（p>0）；焦点在X轴上的抛物线的标准方程可以设为：Y2=mX（m不等于0）；焦点在Y轴上的抛物线的标准方程可以设为：X2=mY（m不等于0）等。