
分析 (1)区域D:$\left\{\begin{array}{l}{y≤2x}\\{x+y≤n}\\{y≥0}\end{array}\right.$,其中n∈N*.记区域D内的整点个数为an.
n=1时,区域D包括(0,0),(0,1)两个点,可得a1=2,
同理可得:a2=4,a3=7.
(2)an=$\left\{\begin{array}{l}{\frac{{n}^{2}+3n+2}{3},n=3m+1或n=3m+2}\\{\frac{{n}^{2}+3n+3}{3},n=3m+3}\end{array}\right.$,m∈N*.
解答 解:(1)区域D:$\left\{\begin{array}{l}{y≤2x}\\{x+y≤n}\\{y≥0}\end{array}\right.$,其中n∈N*.记区域D内的整点个数为an.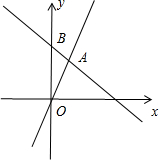
n=1时,区域D包括(0,0),(0,1)两个点,可得a1=2,
同理可得:a2=4,a3=7.
(2)an=$\left\{\begin{array}{l}{\frac{{n}^{2}+3n+2}{3},n=3m+1或n=3m+2}\\{\frac{{n}^{2}+3n+3}{3},n=3m+3}\end{array}\right.$,m∈N*.
点评 本题考查了等差数列的通项公式与求和公式、递推关系、作差法,考查了推理能力与计算能力,属于中档题.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | -9 | C. | -7 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
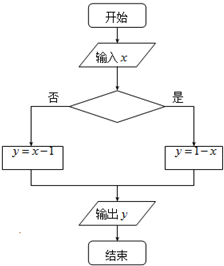 在如图所示的求函数f(x)=|x-1|的函数值的程序框图中,有六名学生在空白处的判断框内填入的条件分别是:①x≥1;②x>1;③x≤1;④x<1;⑤x≥0;⑥x≤0,其中正确的个数是( )
在如图所示的求函数f(x)=|x-1|的函数值的程序框图中,有六名学生在空白处的判断框内填入的条件分别是:①x≥1;②x>1;③x≤1;④x<1;⑤x≥0;⑥x≤0,其中正确的个数是( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
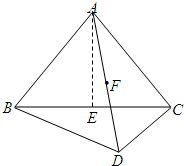 已知四面体ABCD中,AB=AC,BD=CD,平面ABC⊥平面BCD,E,F分别为棱BC和AD的中点.
已知四面体ABCD中,AB=AC,BD=CD,平面ABC⊥平面BCD,E,F分别为棱BC和AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (1,+∞) | C. | (1,+∞)∪(-∞,-1) | D. | (-∞,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com