
(本题16分)在平面直角坐标系 中,
中, 是抛物线
是抛物线 的焦点,
的焦点, 是抛物线
是抛物线 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过 三点的圆的圆心为
三点的圆的圆心为 ,点
,点 到抛物线
到抛物线 的准线的距离为
的准线的距离为 .
.
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)是否存在点 ,使得直线
,使得直线 与抛物线
与抛物线 相切于点
相切于点 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(Ⅲ)若点 的横坐标为
的横坐标为 ,直线
,直线 与抛物线
与抛物线 有两个不同的交点
有两个不同的交点 ,
, 与圆
与圆 有两个不同的交点
有两个不同的交点 ,求当
,求当 时,
时, 的最小值.
的最小值.
(1) ,(2)存在,
,(2)存在, ,
, (3)
最小值
(3)
最小值
【解析】利用抛物线的几何性质、圆的方程以及直线与圆锥曲线的位置关系求解。
试题分析:
(1)由题意,知 ,圆心
,圆心 在线段
在线段 的中垂线
的中垂线 上,抛物线准线方程为
上,抛物线准线方程为 ,所以
,所以 ,得,
,得, ,抛物线方程为
,抛物线方程为 ……………………….4分
……………………….4分
(2)假设存在点 满足条件,抛物线
满足条件,抛物线 在点
在点 处的切线斜率为
处的切线斜率为 ,所以,直线
,所以,直线 ,令
,令 ,得
,得 ,故
,故 ,
,
又 ,得,
,得, ,由
,由 ,解得
,解得 ,
, 满足条件。…………………………………………8分
满足条件。…………………………………………8分
(3)当 时,由(2)知
时,由(2)知 ,圆
,圆 的半径
的半径 ,
,
圆 设
设 ,
, 由
由 ,整理得
,整理得
 ,
, ,
,
设 ,
, 由
由 ,整理得
,整理得 ,
,
 ,令
,令 ,
, ,
, ,
,
 ,
,
 ,当
,当 时,
时,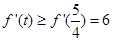 ,
, 在
在 递增,故当
递增,故当 ,即
,即 时,有最小值
时,有最小值 ……………………………………………………………….16分
……………………………………………………………….16分
考点:本题主要考查了抛物线的几何性质、圆的方程以及直线与圆锥曲线的位置关系等,综合考查了学生的运算求解能力和推理论证能力。
点评:解决此题的关键是掌握抛物线的几何性质、圆的方程以及直线与圆锥曲线的位置关系等知识以及较强的运算求解能力和推理论证能力,难度很大。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
(本题满分16分)
在平面直角坐标系![]() 中,已知圆心在第二象限、半径为
中,已知圆心在第二象限、半径为![]() 的圆
的圆![]() 与直线
与直线![]() 相切于坐标原点
相切于坐标原点![]() .椭圆
.椭圆![]() 与圆
与圆![]() 的一个交点到椭圆两焦点的距离之和为
的一个交点到椭圆两焦点的距离之和为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)试探究圆![]() 上是否存在异于原点的点
上是否存在异于原点的点![]() ,使
,使![]() 到椭圆右焦点
到椭圆右焦点![]() 的距离等于线段
的距离等于线段![]() 的长.若存在,请求出点
的长.若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分16分)在平面直角坐标系![]() 中,已知圆心在第二象限、半径为
中,已知圆心在第二象限、半径为![]() 的圆
的圆![]() 与直线
与直线![]() 相切于坐标原点
相切于坐标原点![]() .椭圆
.椭圆![]() 与圆
与圆![]() 的一个交点到椭圆两焦点的距离之和为
的一个交点到椭圆两焦点的距离之和为![]() .
.
(1)求圆![]() 的方程;
的方程;
查看答案和解析>>
科目:高中数学 来源:2013届江苏省南通市高二期中联考数学试卷 题型:解答题
(本题满分16分)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点, =2
=2 =2.
=2.
(1)求证: ;
;
(2)求证: ∥平面
∥平面 ;
;
(3)求三棱锥 的体积
的体积 .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分16分 )
在平面直角坐标系中,椭圆C:![]() (a>b>0),圆O:x2+y2=a2,且过点A(,0)所作圆的两条切线互相垂直.
(a>b>0),圆O:x2+y2=a2,且过点A(,0)所作圆的两条切线互相垂直.
(Ⅰ)求椭圆离心率;
(Ⅱ)若直线y=2与圆交于D、E;与椭圆交于M、N,且DE=2MN,求椭圆的方程;
(Ⅲ)设点T(0,3)在椭圆内部,若椭圆C上的点到点P的最远距离不大于5,求椭圆C的短轴长的取值范围.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com