
【题目】已知不等式ax2+5x+b>0的解集是{x|2<x<3},则不等式bx2﹣5x+a>0的解集是( )
A.{x|x<﹣3或x>﹣2}
B.{x|x<﹣ ![]() 或x>﹣
或x>﹣ ![]() }
}
C.{x|﹣ ![]() <x<﹣
<x<﹣ ![]() }
}
D.{x|﹣3<x<﹣2}
【答案】C
【解析】解:不等式ax2+5x+b>0的解集是{x|2<x<3},∴方程ax2+5x+b=0的实数根为2和3,
∴ 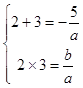 ,
,
解得a=﹣1,b=﹣6;
∴不等式bx2﹣5x+a>0为﹣6x2﹣5x﹣1>0,
即6x2+5x+1<0,
解得﹣ ![]() <x<﹣
<x<﹣ ![]() ;
;
∴不等式bx2﹣5x+a>0的解集是{x|﹣ ![]() <x<﹣
<x<﹣ ![]() }.
}.
故选:C.
【考点精析】认真审题,首先需要了解解一元二次不等式(求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边).
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边).


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(2+x),g(x)=ln(2﹣x)
(1)判断函数h(x)=f(x)﹣g(x)的奇偶性;
(2)求使f(x)≥g(x)成立的x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的方格纸由若干个边长为1的小正方形并在一起组成,方格纸中有两个定点A,B,点C为小正方形的顶点,且 ![]()
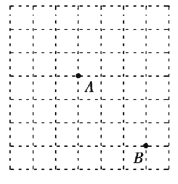
(1)画出所有的向量 ![]() ;
;
(2)求| ![]() |的最大值与最小值.
|的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
直角坐标系中曲线![]() 的参数方程
的参数方程![]() (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点, ![]() 轴正半轴为极轴的极坐标系中,
轴正半轴为极轴的极坐标系中, ![]() 点的极坐标
点的极坐标![]() ,在平面直角坐标系中,直线
,在平面直角坐标系中,直线![]() 经过点
经过点![]() ,倾斜角为
,倾斜角为![]()
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (p,q为常数)是定义在(﹣1,1)上的奇函数,且
(p,q为常数)是定义在(﹣1,1)上的奇函数,且 ![]() .
.
(1)求函数f(x)的解析式;
(2)判断并用定义证明f(x)在(﹣1,1)上的单调性;
(3)解关于x的不等式f(2x﹣1)+f(x)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x,g(x)=ax+2(a>0),若对任意x1∈R,都存在x2∈[﹣2,+∞),使得f(x1)>g(x2),则实数a的取值范围是( )
A.![]()
B.(0,+∞)
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位: ![]() )有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间
)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为200瓶,为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶,为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 |
|
|
|
|
|
|
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量![]() (单位:瓶)的分布列;
(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为![]() (单位:元).当六月份这种酸奶一天的进货量(单位:瓶)为多少时,
(单位:元).当六月份这种酸奶一天的进货量(单位:瓶)为多少时, ![]() 的数学期望达到最大值?
的数学期望达到最大值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com