
【题目】已知函数 ![]() (p,q为常数)是定义在(﹣1,1)上的奇函数,且
(p,q为常数)是定义在(﹣1,1)上的奇函数,且 ![]() .
.
(1)求函数f(x)的解析式;
(2)判断并用定义证明f(x)在(﹣1,1)上的单调性;
(3)解关于x的不等式f(2x﹣1)+f(x)<0.
【答案】
(1)解:依题意, 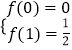 ,解得p=1,q=0,所以
,解得p=1,q=0,所以 ![]() .
.
(2)解:函数f(x)在(﹣1,1)上单调递增,证明如下:
任取﹣1<x1<x2<1,则x1﹣x2<0,﹣1<x1x2<1,
从而f(x1)﹣f(x2)= ![]() ﹣
﹣ ![]() =
= ![]() =
= ![]() <0,
<0,
所以f(x1)<f(x2),
所以函数f(x)在(﹣1,1)上单调递增.
(3)解:原不等式可化为:f(2x﹣1)<﹣f(x),即f(2x﹣1)<f(﹣x),
由(2)可得,函数f(x)在(﹣1,1)上单调递增,所以 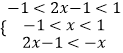 ,
,
解得 ![]() ,即原不等式解集为
,即原不等式解集为 ![]()
【解析】(1)依题意, 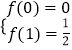 ,解得p=1,q=0,可得函数的解析式.(2)利用函数的单调性的定义证明函数f(x)在(﹣1,1)上单调递增.(3)原不等式可化为f(2x﹣1)<f(﹣x),根据函数f(x)在定义域(﹣1,1)上单调递增,可得
,解得p=1,q=0,可得函数的解析式.(2)利用函数的单调性的定义证明函数f(x)在(﹣1,1)上单调递增.(3)原不等式可化为f(2x﹣1)<f(﹣x),根据函数f(x)在定义域(﹣1,1)上单调递增,可得 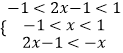 ,由此求得x的范围.
,由此求得x的范围.
【考点精析】关于本题考查的函数单调性的判断方法和函数单调性的性质,需要了解单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】如图,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,
点, ![]() 为弦
为弦![]() 的中点,直线
的中点,直线![]() 分别与直线
分别与直线![]() 和直线
和直线![]() 交于
交于![]() 两点.
两点.
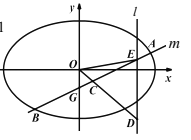
(1)求直线![]() 的斜率和直线
的斜率和直线![]() 的斜率之积;
的斜率之积;
(2)分别记![]() 和
和![]() 的面积为
的面积为![]() ,是否存在正数
,是否存在正数![]() ,使得
,使得![]() 若存在,求出
若存在,求出![]() 的取值;若不存在,说明理由.
的取值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式ax2+5x+b>0的解集是{x|2<x<3},则不等式bx2﹣5x+a>0的解集是( )
A.{x|x<﹣3或x>﹣2}
B.{x|x<﹣ ![]() 或x>﹣
或x>﹣ ![]() }
}
C.{x|﹣ ![]() <x<﹣
<x<﹣ ![]() }
}
D.{x|﹣3<x<﹣2}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个顶点A、B、C及平面内一点P满足 ![]() +
+ ![]() =
= ![]() ,下列结论中正确的是( )
,下列结论中正确的是( )
A.P在△ABC的内部
B.P在△ABC的边AB上
C.P在AB边所在直线上
D.P在△ABC的外部
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx﹣x2+1.
(Ⅰ)若曲线y=f(x)在x=1处的切线方程为4x﹣y+b=0,求实数a和b的值;
(Ⅱ)讨论函数f(x)的单调性;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P﹣ABC中,已知PA=PB=PC=AC=4,BC= ![]() AB=2
AB=2 ![]() ,O为AC中点.
,O为AC中点. 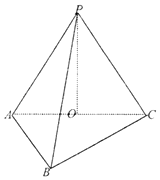
(1)求证:PO⊥平面ABC;
(2)求异面直线AB与PC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (m,n为常数)是定义在[﹣1,1]上的奇函数,且f(﹣1)=﹣
(m,n为常数)是定义在[﹣1,1]上的奇函数,且f(﹣1)=﹣ ![]() .
.
(1)求函数f(x)的解析式;
(2)解关于x的不等式f(2x﹣1)<﹣f(x).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com