
【题目】设函数![]() ,m∈R.
,m∈R.
(Ⅰ)当m=e(e为自然对数的底数)时,求f(x)的极小值;
(Ⅱ)讨论函数![]() 零点的个数.
零点的个数.
【答案】(1)当x=e时,f(x)取得极小值2(2)见解析
【解析】试题分析:(1)求函数的导数![]() ,函数的极值点为
,函数的极值点为![]() ,所以得到函数的单调区间,也就得到函数的最小值了;(2)根据
,所以得到函数的单调区间,也就得到函数的最小值了;(2)根据![]() ,参变分离后得到
,参变分离后得到![]() ,设
,设![]() ,通过导数求函数的单调性,以及图象特征,转化为
,通过导数求函数的单调性,以及图象特征,转化为![]() 与函数的交点个数问题.
与函数的交点个数问题.
试题解析:(1)当![]() 时,
时, ![]() ,∴
,∴![]()
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是减函数;
上是减函数;
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是增函;
上是增函;
∴当![]() 时,
时, ![]() 取最小值
取最小值![]() .
.
(2)∵函数![]() ,
,
令![]() ,得
,得![]() ;
;
设![]() ,则
,则![]()
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是增函数;
上是增函数;
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是减函数;
上是减函数;
当![]() 是
是![]() 的极值点,且是唯一极大值点,∴
的极值点,且是唯一极大值点,∴![]() 是
是![]() 的最大值点;
的最大值点;
∴![]() 的最大值为
的最大值为![]() ,又
,又![]() 结合
结合![]() 的图像,
的图像,
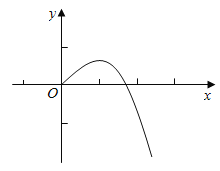
可知:
①当![]() 时,函数
时,函数![]() 无零点;
无零点;
②当![]() 时,函数
时,函数![]() 有且只有一个零点;
有且只有一个零点;
③当![]() 时,函数
时,函数![]() 有两个零点;
有两个零点;
④当![]() 时,函数
时,函数![]() 有且只有一个零点;
有且只有一个零点;
综上:
当![]() 时,函数
时,函数![]() 无零点;当
无零点;当![]() 或
或![]() 时,函数
时,函数![]() 有且只有一个零点;当
有且只有一个零点;当![]() 时,函数
时,函数![]() 有且只有两个零点.
有且只有两个零点.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
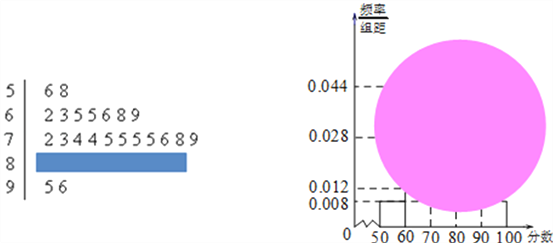
(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间矩形的高;
(Ⅲ)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在[90,100)之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一大学生自主创业,拟生产并销售某电子产品![]() 万件(生产量与销售量相等),为扩大影响进行促销,促销费用
万件(生产量与销售量相等),为扩大影响进行促销,促销费用![]() (万元)满足
(万元)满足![]() (其中
(其中![]() 为正常数).已知生产该产品还需投入成本
为正常数).已知生产该产品还需投入成本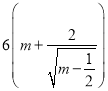 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为![]() 元/件.
元/件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,此大学生所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的方格纸由若干个边长为1的小正方形并在一起组成,方格纸中有两个定点A,B,点C为小正方形的顶点,且 ![]()
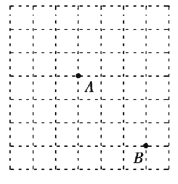
(1)画出所有的向量 ![]() ;
;
(2)求| ![]() |的最大值与最小值.
|的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|x>1},B={x|x≥2}.
(1)求集合A∩(RB);
(2)若集合C={x|x﹣a>0},且满足A∩C=C,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
直角坐标系中曲线![]() 的参数方程
的参数方程![]() (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点, ![]() 轴正半轴为极轴的极坐标系中,
轴正半轴为极轴的极坐标系中, ![]() 点的极坐标
点的极坐标![]() ,在平面直角坐标系中,直线
,在平面直角坐标系中,直线![]() 经过点
经过点![]() ,倾斜角为
,倾斜角为![]()
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (p,q为常数)是定义在(﹣1,1)上的奇函数,且
(p,q为常数)是定义在(﹣1,1)上的奇函数,且 ![]() .
.
(1)求函数f(x)的解析式;
(2)判断并用定义证明f(x)在(﹣1,1)上的单调性;
(3)解关于x的不等式f(2x﹣1)+f(x)<0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com