
【题目】设集合A={x|x>1},B={x|x≥2}.
(1)求集合A∩(RB);
(2)若集合C={x|x﹣a>0},且满足A∩C=C,求实数a的取值范围.
【答案】
(1)解:由题意得,B={x|x≥2},
则RB={x|x<2},
又A={x|x>1},所以A∩(RB)={x|1<x<2}
(2)解:C={x|x﹣a>0}={x|x>a},
由A∩C=C得,CA,
所以a≥1,即实数a的取值范围是[1,+∞)
【解析】(1)由题意和补集的运算求出RB,由交集的运算求出A∩(RB);(2)先求出集合C,由A∩C=C得CA,根据子集的定义求出实数a的取值范围.
【考点精析】根据题目的已知条件,利用集合的交集运算和交、并、补集的混合运算的相关知识可以得到问题的答案,需要掌握交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立;求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法.
B,反之也成立;求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:
【题目】经市场调查:生产某产品需投入年固定成本为3万元,每生产x万件,需另投入流动成本为W(x)万元,在年产量不足8万件时,W(x)= ![]() x2+x(万元),在年产量不小于8万件时,W(x)=6x+
x2+x(万元),在年产量不小于8万件时,W(x)=6x+ ![]() ﹣38(万元).通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
﹣38(万元).通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(1)写出年利润L(x)(万元)关于年产量x(万件)的函数解析式;
(2)写出当产量为多少时利润最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集为R,集合A=(﹣∞,﹣1)∪(3,+∞),记函数f(x)= ![]() 的定义域为集合B
的定义域为集合B
(1)分别求A∩B,A∩RB;
(2)设集合C={x|a+3<x<4a﹣3},若B∩C=C,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】Rt△ABC的斜边BC在平面α内,则△ABC的两条直角边在平面α内的正射影与斜边组成的图形只能是( )
A.一条线段
B.一个锐角三角形或一条线段
C.一个钝角三角形或一条线段
D.一条线段或一个钝角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校毕业典礼由6个节目组成,考虑整体效果,对节目演出顺序有如下要求:节目甲必须排在前三位,且节目丙、丁必须排在一起,则该校毕业典礼节目演出顺序的编排方案共有
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
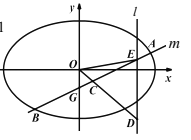
【题目】如图,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,
点, ![]() 为弦
为弦![]() 的中点,直线
的中点,直线![]() 分别与直线
分别与直线![]() 和直线
和直线![]() 交于
交于![]() 两点.
两点.
(1)求直线![]() 的斜率和直线
的斜率和直线![]() 的斜率之积;
的斜率之积;
(2)分别记![]() 和
和![]() 的面积为
的面积为![]() ,是否存在正数
,是否存在正数![]() ,使得
,使得![]() 若存在,求出
若存在,求出![]() 的取值;若不存在,说明理由.
的取值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个顶点A、B、C及平面内一点P满足 ![]() +
+ ![]() =
= ![]() ,下列结论中正确的是( )
,下列结论中正确的是( )
A.P在△ABC的内部
B.P在△ABC的边AB上
C.P在AB边所在直线上
D.P在△ABC的外部
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2+mx+n(m、n∈R)的两个零点分别在(0,1)与(1,2)内,则(m+1)2+(n﹣2)2的取值范围是( )
A.![]()
B.![]()
C.[2,5]
D.(2,5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com