
 的图像向右平移
的图像向右平移 个单位长度后,再使平移后的图像纵坐标不变,
个单位长度后,再使平移后的图像纵坐标不变, 的图像,将方程
的图像,将方程 的所有正根按从小到大排成一个数列
的所有正根按从小到大排成一个数列 ,在以下结论中: ①
,在以下结论中: ① ;
;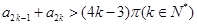 ;③
;③ .
.| A.0 | B.1 | C.2 | D.3 |
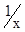 的图象在第一象限的交点横坐标,然后画出两函数的图形,结合图形可判定选项的真假.
的图象在第一象限的交点横坐标,然后画出两函数的图形,结合图形可判定选项的真假.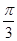 )的图象向右平移
)的图象向右平移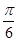 个单位长度后,
个单位长度后,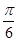 )+
)+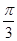 ]=sin2x,
]=sin2x,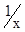 的图象在第一象限的交点横坐标
的图象在第一象限的交点横坐标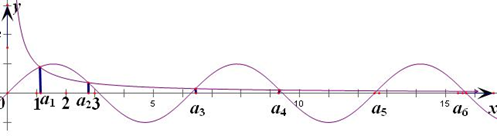
| lim |
| n→∞ |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com