
| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | $\frac{4\sqrt{2}-\sqrt{6}}{2}$ | D. | 2$\sqrt{2}$-1 |
分析 写出椭圆的参数方程$\left\{\begin{array}{l}{x=\sqrt{3}cosα}\\{y=sinα}\end{array}\right.$(0≤α<2π),设出点P的坐标,运用点到直线的距离公式,以及两角和的正弦公式,结合正弦函数的最值,即可得到答案.
解答 解:由于椭圆$\frac{{x}^{2}}{3}$+y2=1的参数方程为:参数方程$\left\{\begin{array}{l}{x=\sqrt{3}cosα}\\{y=sinα}\end{array}\right.$(0≤α<2π),设点P($\sqrt{3}$cosα,sinα),
则P到直线l:x+y-4=0的距离为d=$\frac{|\sqrt{3}cosα+sinα-4|}{\sqrt{2}}$=$\frac{|2sin(α+\frac{π}{3})-4|}{\sqrt{2}}$.
则当sin(α+$\frac{π}{3}$)=-1时,d取得最大值:3$\sqrt{2}$.
故选:B.
点评 本题考查直线与椭圆的位置关系,解题时要认真审题,注意椭圆的参数方程、点到直线的距离公式、三角函数的性质的灵活运用.


 培优三好生系列答案
培优三好生系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $-\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
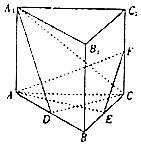 如图,在正三棱柱ABC-A1B1C1中,E、F分别是BC、CC1的中点.
如图,在正三棱柱ABC-A1B1C1中,E、F分别是BC、CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤-1} | B. | {x|x≥3} | C. | {x|x≤-1或x≥3} | D. | {x|x≤0或x≥3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
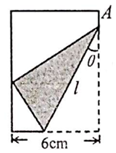 如图,将矩形纸片的右下角折起,使得该角的顶点落在矩形的左边上,若$sinθ=\frac{1}{4}$,则折痕l的长度=$\frac{64}{5}$cm.
如图,将矩形纸片的右下角折起,使得该角的顶点落在矩形的左边上,若$sinθ=\frac{1}{4}$,则折痕l的长度=$\frac{64}{5}$cm.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com