
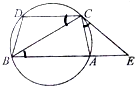
 如图,已知圆上是弧AC=弧BD,过点C的圆的切线CE与BA的延长线交于点E.
如图,已知圆上是弧AC=弧BD,过点C的圆的切线CE与BA的延长线交于点E.分析 (1)先根据题中条件弧AC=弧BD得∠BCD=∠ABC.再根据EC是圆的切线,得到∠ACE=∠ABC,从而即可得出结论.
(2)欲证BD2=AE×CD.即证$\frac{BD}{AE}=\frac{DC}{AC}$,.故只须证明△BDC~△EAC即可.
解答 解:(1)因为弧AC=弧BD,
所以∠BCD=∠ABC.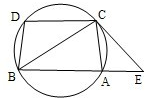
又因为EC与圆相切于点C,
故∠ACE=∠ABC
所以∠ACE=∠BCD.(5分)
(Ⅱ)因为∠CAE=∠CDB,∠EBC=∠BCD,
所以△BDC~△EAC,
故$\frac{BD}{AE}=\frac{DC}{AC}$.
因为BD=AC
所以BD2=AE×CD.(10分)
点评 本题主要考查圆的切线的判定定理的证明、弦切角的应用、三角形相似等基础知识,考查运化归与转化思想.属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)>f(2) | B. | f(1)<f(2) | ||
| C. | f(1)=f(2) | D. | f(1)与f(2)大小无法判定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校为了解高一新生对文理科的选择,对1000名高一新生发放文理科选择调查表,统计知,有600名学生选择理科,400名学生选择文科.分别从选择理科和文科的学生随机各抽取20名学生的数学成绩得如下累计表:
某校为了解高一新生对文理科的选择,对1000名高一新生发放文理科选择调查表,统计知,有600名学生选择理科,400名学生选择文科.分别从选择理科和文科的学生随机各抽取20名学生的数学成绩得如下累计表:| 分数段 | 理科人数 | 文科人数 |
| [40,50) |  | |
| [50,60) | 一 | 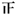 |
| [60,70) | 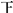 | 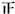 |
| [70,80) | 正 一 | 正 |
| [80,90) | 正 一 | 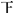 |
| [90,100] | 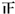 | 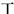 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 没选统计专业 | 选统计专业 | |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com