
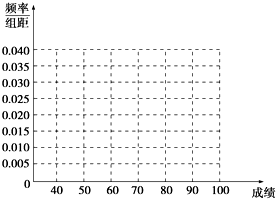
 某校为了解高一新生对文理科的选择,对1000名高一新生发放文理科选择调查表,统计知,有600名学生选择理科,400名学生选择文科.分别从选择理科和文科的学生随机各抽取20名学生的数学成绩得如下累计表:
某校为了解高一新生对文理科的选择,对1000名高一新生发放文理科选择调查表,统计知,有600名学生选择理科,400名学生选择文科.分别从选择理科和文科的学生随机各抽取20名学生的数学成绩得如下累计表:| 分数段 | 理科人数 | 文科人数 |
| [40,50) | 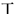 | |
| [50,60) | 一 | 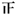 |
| [60,70) | 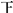 | 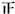 |
| [70,80) | 正 一 | 正 |
| [80,90) | 正 一 | 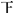 |
| [90,100] | 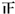 | 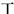 |
分析 (1)从统计表看出选择理科的学生的数学平均成绩高于选择文科的学生的数学平均成绩,反映了数学成绩对学生选择文理科有一定的影响;
(2)利用互斥事件的加法公式,即可得出结论.
解答 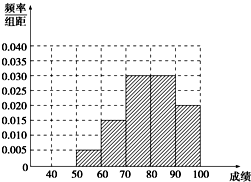 解:(1)从统计表看出选择理科的学生的数学平均成绩高于选择文科的学生的数学平均成绩,反映了数学成绩对学生选择文理科有一定的影响,频率分布直方图如右.
解:(1)从统计表看出选择理科的学生的数学平均成绩高于选择文科的学生的数学平均成绩,反映了数学成绩对学生选择文理科有一定的影响,频率分布直方图如右.
(2)设选择理科的学生考分在[70,80),[80,90),[90,100]分别为事件A1,A2,A3选择文科的学生考分在[70,80),[80,90),[90,100]的事件分别为B1,B2,B3,事件C=选取理科学生的数学成绩一定至少高于选取文科的学生的数学成绩一个分数段.
则C=A2B1+A3(B1∪B2),∴P(C)=P(A2)•P(B1)+P(A3)(P(B1)+P(B2)),
由累计表可得P(C)=$\frac{6}{16}$×$\frac{5}{10}$+$\frac{4}{16}$×($\frac{5}{10}$+$\frac{3}{10}$)=$\frac{31}{80}$.
点评 本题考查频率分布直方图,考查概率的求法,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
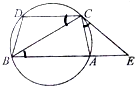 如图,已知圆上是弧AC=弧BD,过点C的圆的切线CE与BA的延长线交于点E.
如图,已知圆上是弧AC=弧BD,过点C的圆的切线CE与BA的延长线交于点E.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 随机误差由解释变量和预报变量共同确定 | |
| B. | 预报变量只由解释变量确定 | |
| C. | 预报变量由解释变量和随机误差共同确定 | |
| D. | 随机误差只由预报变量确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com