
分析 结合图象通过讨论直线y=x+b的位置,求出b的范围即可.
解答 解:曲线方程变形为(x-2)2+(y-3)2=4,表示圆心A为(2,3),半径为2的下半圆,
根据题意画出图形,如图所示: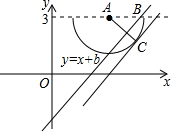 ,
,
当直线y=x+b过B(4,3)时,将B坐标代入直线方程得:3=4+b,即b=-1;
当直线y=x+b与半圆相切时,圆心A到直线的距离d=r,
即$\frac{|b-1|}{\sqrt{2}}$=2,即b-1=2$\sqrt{2}$(不合题意舍去)或b-1=-2$\sqrt{2}$,
解得:b=1-2$\sqrt{2}$,
则直线与曲线有两个公共点时b的范围为1-2$\sqrt{2}$<b≤-1.
故答案为:1-2$\sqrt{2}$<b≤-1.
点评 本题考查了直线和圆锥曲线的关系,考查二次函数的性质,是一道中档题.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. |  | B. | 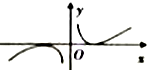 | ||
| C. | 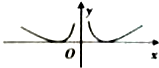 | D. | 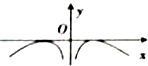 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
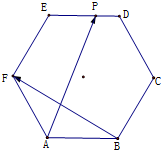 如图,正六边形ABCDEF的边长为2,P是线段DE上的任意一点,则$\overrightarrow{AP}$•$\overrightarrow{BF}$的取值范围为[0,6]..
如图,正六边形ABCDEF的边长为2,P是线段DE上的任意一点,则$\overrightarrow{AP}$•$\overrightarrow{BF}$的取值范围为[0,6]..查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{5}}}{2}$ | B. | $3\sqrt{5}$ | C. | $\frac{{3\sqrt{7}}}{2}$ | D. | $3\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,且AB=4,BC=CD=ED=EA=2.
如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,且AB=4,BC=CD=ED=EA=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)>f(2) | B. | f(1)<f(2) | ||
| C. | f(1)=f(2) | D. | f(1)与f(2)大小无法判定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校为了解高一新生对文理科的选择,对1000名高一新生发放文理科选择调查表,统计知,有600名学生选择理科,400名学生选择文科.分别从选择理科和文科的学生随机各抽取20名学生的数学成绩得如下累计表:
某校为了解高一新生对文理科的选择,对1000名高一新生发放文理科选择调查表,统计知,有600名学生选择理科,400名学生选择文科.分别从选择理科和文科的学生随机各抽取20名学生的数学成绩得如下累计表:| 分数段 | 理科人数 | 文科人数 |
| [40,50) |  | |
| [50,60) | 一 |  |
| [60,70) | 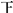 | 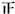 |
| [70,80) | 正 一 | 正 |
| [80,90) | 正 一 | 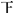 |
| [90,100] | 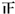 | 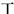 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com