
【题目】已知命题p:指数函数f(x)=(m+1)x是减函数;命题q:x∈R,x2+x+m<0,若“p或q”是真命题,则实数m的取值范围是 .
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥 ![]() 的底面为直角梯形,
的底面为直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 底面
底面 ![]() ,
, ![]() 为
为 ![]() 的中点.
的中点.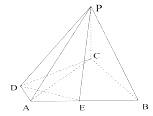
(Ⅰ)求证:平面 ![]() 平面
平面 ![]()
(Ⅱ)求直线 ![]() 与平面
与平面 ![]() 所成的角的正弦值.
所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
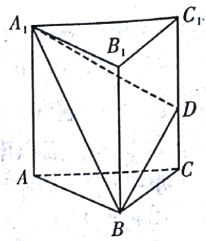
【题目】如图,已知三棱柱![]() 的所有棱长都相等,且侧棱垂直于底面,由
的所有棱长都相等,且侧棱垂直于底面,由![]() 沿棱柱侧面经过棱
沿棱柱侧面经过棱![]() 到点
到点![]() 的最短路线长为
的最短路线长为![]() ,设这条最短路线与
,设这条最短路线与![]() 的交点为
的交点为![]() .
.
(1)求三棱柱![]() 的体积;
的体积;
(2)证明:平面![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半圆AOB是某市休闲广场的平面示意图,半径OA的长为10,管理部门在A,B两处各安装好一个光源,其相应的光强度分别为4和9,根据光学原理,地面上某处照度y与光强度I成正比,与光源距离x的平方成反比,即y= ![]() (k为比例系数),经测量,在弧AB的中心C处的照度为130.(C处的照度为A,B两处光源的照度之和)
(k为比例系数),经测量,在弧AB的中心C处的照度为130.(C处的照度为A,B两处光源的照度之和) 
(1)求比例系数k的值;
(2)现在管理部门计划在半圆弧AB上,照度最小处增设一个光源P,试问新增光源P安装在什么位置?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,且
,且![]() ).
).
(1)当![]() 时,设集合
时,设集合![]() ,求集合
,求集合![]() ;
;
(2)在(1)的条件下,若![]() ,且满足
,且满足![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若对任意的![]() ,存在
,存在![]() ,使不等式
,使不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下判断: ①f(x)= ![]() 与g(x)=
与g(x)= ![]() 表示同一函数;
表示同一函数;
②函数y=f(x)的图象与直线x=1的交点最多有1个;
③f(x)=x2﹣2x+1与g(t)=t2﹣2t+1是同一函数;
④若f(x)=|x﹣1|﹣|x|,则f(f( ![]() ))=0.
))=0.
其中正确判断的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com