
【题目】有以下判断: ①f(x)= ![]() 与g(x)=
与g(x)= ![]() 表示同一函数;
表示同一函数;
②函数y=f(x)的图象与直线x=1的交点最多有1个;
③f(x)=x2﹣2x+1与g(t)=t2﹣2t+1是同一函数;
④若f(x)=|x﹣1|﹣|x|,则f(f( ![]() ))=0.
))=0.
其中正确判断的序号是 .
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx﹣ax,a∈R.
(1)当x=1时,函数f(x)取得极值,求a的值;
(2)当0<a< ![]() 时,求函数f(x)在区间[1,2]上的最大值;
时,求函数f(x)在区间[1,2]上的最大值;
(3)当a=﹣1时,关于x的方程2mf(x)=x2(m>0)有唯一实数解,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一种新型的洗衣液,去污速度特别快.已知每投放![]() (
(![]() 且
且![]() )个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度
)个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (分钟) 变化的函数关系式近似为
(分钟) 变化的函数关系式近似为![]() ,其中
,其中 .根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.
.根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.
(1)若投放![]() 个单位的洗衣液,3分钟时水中洗衣液的浓度为4 (克/升),求
个单位的洗衣液,3分钟时水中洗衣液的浓度为4 (克/升),求![]() 的值;
的值;
(2)若投放4个单位的洗衣液,则有效去污时间可达几分钟?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() 且
且![]() ),当点
),当点![]() 是函数
是函数![]() 图象上的点时,点
图象上的点时,点![]() 是函数
是函数![]() 图象上的点.
图象上的点.
(1)写出函数![]() 的解析式;
的解析式;
(2)把![]() 的图象向左平移
的图象向左平移![]() 个单位得到
个单位得到![]() 的图象,函数
的图象,函数![]() ,是否存在实数
,是否存在实数![]() ,使函数
,使函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() .如果存在,求出
.如果存在,求出![]() 的值;如果不存在,说明理由;
的值;如果不存在,说明理由;
(3)若当![]() 时,恒有
时,恒有![]() ,试确定
,试确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧面AA1C1C底面ABC,AA1=A1C=AC=AB=BC=2,且点O为AC中点. 
(Ⅰ)证明:A1O⊥平面ABC;
(Ⅱ)求二面角A1﹣AB﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国个人所得税法》规定,公民全月工资、薪金(扣除三险一金后)所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额个人所得税计算公式:应纳税额=工资-三险一金=起征点. 其中,三险一金标准是养老保险8%、医疗保险2%、失业保险1%、住房公积金8%,此项税款按下表分段累计计算:
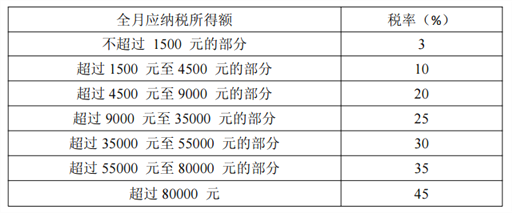
(1)某人月收入15000元(未扣三险一金),他应交个人所得税多少元?
(2)某人一月份已交此项税款为1094元,那么他当月的工资(未扣三险一金)所得是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com